Relations and Functions

A relation is a connection between the elements of a set or the elements of two sets.

e.g. "is greater than" and " is twice the size of " are examples of relations.

A function is a special type of relation.

Representation

Relations can be represented in several ways:

  • As a set of ordered pairs.

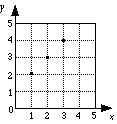
e.g. A = {(1, 2), (2, 3), (3, 4)}

The first value in each ordered pair is the x-value.

The second value in each ordered pair is the y-value.

  • As an arrow graph or mapping.

    e.g. The domain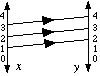Y10_Relations_and_Functions_01.gifThe range

The set of x-values is called the domain. i.e. {1, 2, 3}

The set of y-values is called the range. i.e. {2, 3, 4}

  • In table form

    e.g.

Domain
Range
x
y
1
2
2
3
3
4

 

    • On a graph.

e.g.Y10_Relations_and_Functions_02.gif

  • By a rule or formula.

    e.g. y = x + 1

A function is a relation where each of the members of the domain,(each x value) is connected to only one member of the range, (the y value). Most relations are also functions.

Exceptions are relations such as x 2 + y 2 = 9 which has a graph of a circle. This relation is not a function.

Sequences

In mathematics, numbers are often arranged in a sequence. These sequences can be shown be a formula or function.

Often a sequence follows a rule or pattern.

Easy Sequence
Some sequences are obvious: 2, 4, 6, 8, 10...
This is the sequence of EVEN numbers.

The formula for this sequence is 2n where n stands for a counting number.

To find the next number in this sequence, calculate 2 × 6 = 12

Slightly Harder Sequence
The sequence 1, 4, 9, 16, 25... is the sequence of square numbers.
Comparing this sequence to the set of counting numbers {1, 2, 3, 4..}

1
2
3
4
5
...
1
4
9
16
25
...

The formula for this sequence is n2.
The next number in this sequence is 62 = 36

 

 

More Difficult Sequence
The number of diagonals in polygons forms a sequence.

Name of polygon
Triangle
Quadrilateral
Pentagon
Hexagon
Heptagon
Number of sides
3
4
5
6
7
Number of diagonals
0
2
5
9
14

The sequence for the number of diagonals is 0, 2, 5, 9, 14...
The pattern for this sequence is an increase of 2, 3, 4 between each term.
The formula for this sequence is (n2 + n − 2)/2
The next number in this sequence is 20