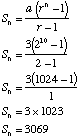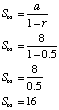If terms of a geometric sequence are added together a geometric series is formed.
2 + 4 + 8 + 16 is a finite geometric series
2 + 4 + 8 + 16 + ... is an infinte geometric series
To find the sum of the first n terms of a geometric sequence use the formula:
|
Sum of first n terms of geometric sequence where |
|
OR
If the common ratio is a fraction i.e. -1 < r < 1 then an equivalent formula, shown below is easier to use.
|
Sum of first n terms of geometric sequence for when -1 < r < 1 i.e. r is a fraction |
|
Example What is the sum of the first 10 terms of the geometric sequence: 3, 6, 12, ...
|
|
The Sum to Infinity of a Geometric Sequence
Spreadsheets are very useful for generating sequences and series.
For a geometric sequence with a common ratio greater than 1:
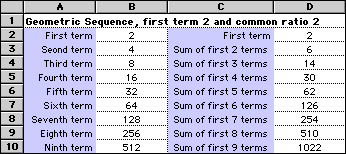 |
The formula in cell B3 is = B2*2 The formula in cell D3 is =D2 + B3 The fill down command is then used to complete the sequences. |
It can be seen that as successive terms are added the sum of the terms increases.
If there were an infinite number of terms the sum would be infinity.
For a geometric sequence with a common ratio less than 1:
 |
The formula in cell B3 is = B2*0.5 The formula in cell D3 is =D2 + B3 The fill down command is then used to comlete the sequences. |
It can be seen that as successive terms are added the sum of the terms appears to be heading towards 16.
If there were an infinite number of terms the sum would be 16.
To see this concept clearly illustrated,- ![]()
This is called the sum to infinity of a geometric sequence and only applies when the common ratio is a fraction.
The following formula can be used:
|
Sum to infinity of geometric sequence where |
|
Example
Find the sum to infinity of the geometric sequence 8, 4, 2, 1, ...
a = 8 and r = 0.5
As can be seen from cell D10 in the spreadsheet above, 16 is the value the sums were heading towards.