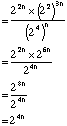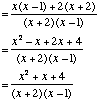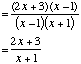In Year 11 (NZ Year 12), the following topics were extensively covered and it is assumed that students will have a thorough understanding of the content covered below.
|
Topic 1
|
|||
| Formulae | |||
|
Topic 17
|
Arithmetic Series | ||
|
Topic 18
|
Geometric Series |
The next few topics in the Mathematics with Calculus course will concentrate on more advanced examples from the above topics.
Expanding Brackets
- If there are three or more brackets , the best method is to multipy two together first and then the third etc.
- If surds are involved then remember √a x √b = √ab
|
Example 1
|
Expand (x + 1)(x − 3)2 |
(x + 1)(x − 3)2
|
= (x + 1)(x − 3)(x − 3) = (x2 − 2x − 3)(x − 3) = x3 − 2x2 − 3x − 3x2 + 6x + 9 = x3 − 5x2 + 3x + 9 |
|
Example 2
|
Expand (√2 + 3)(√2 − 3) |
(√2 + 3)(√2 − 3)
|
= 2 + 3√2 − 3√2 − 9 = 2 − 7 = -5 |
Simplifying Expressions
- The laws of indices apply
- Look for common factors
- Like factors from the numerator and denominator can be cancelled.
| Example 1 | Simplify  |
 |
|
| Example 2 | Simplify  |
 |
|
| Example 3 | Simplify  |
 |
|
Sum and Difference of Two Cubes
The following two factorisations are sometimes useful:
|
The sum of two cubes: x3 + y3 = (x + y)(x2 − xy + y2) |
|
The difference of two cubes: x3 – y3 = (x –y)(x2 + xy + y2) |
Example
64a3 − 27b3 = (4a)3 − (3b)3
= (4a − 3b)(16a2 + 12ab + 9b2)
