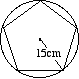
1. A regular pentagon (5-sided figure) is inscribed in a circle of radius 15 cm. What is the length of each side of the pentagon?
2. The quantity Q of a certain chemical in the body varies during the day and is given by the formula Q(t) = 4 + 3cos ![]()
where t measures hours from midnight.
(i) What is the period in hours of the function Q?
(ii) At what time or times of the day is the quantity a minimum?
(iii) What is the minimum quantity of the chemical the body will contain?
(iv) A hospital patient requires a pill to temporarily boost the amount of the chemical whenever the quantity in his body falls to 1.5 units. At what time will a nurse have to wake the patient to give him his first pill of the day?
3. Three points X, Y and Z lie on a straight level path, and XY = YZ = k

The base P of a television mast TP is level with the path. The angles of elevation of the top of the mast from the points X, Y and Z are α, α, and β respectively.
1. Show that the triangle PXY is isosceles.
2. Show that the height h of the mast is
4. (a) The rise and fall of the tide at the jetty on Trig Island is described by y = Acos(0.507t) + B where y = depth of water in metres and t = number of hours after a certain high tide. The water is 8 metres deep at high tide and 2 metres deep at low tide. Work out the values of A and B.
(b) On neighbouring Conic Island the rise and fall of the tide is given by y = 3cos(0.502t) + 4. The ferry boat between the islands requires water at least 3 metres deep. For how long after a high tide can the ferry stay at the Conic Island jetty?
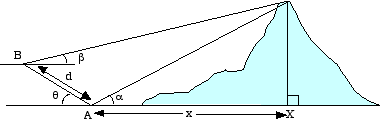
5.. A surveyor wishes to calculate the horizontal distance x from a point A to a point X directly below the top of a hill.

She measures the angle of elevation α of the top of the hill from A and the angle of elevation β from a point B, a horizontal distance d metres further away from the hill, as in the diagram.
a. (i) The distance x is given by:
Use your calculator to evaluate x, to one decimal place, if d = 240 m, α = 24.37°and β = 18.41°.
(ii) Prove that
(Hint: Express the height of the hill in terms of both &alpha and β using the two right-angled triangles.
b. Prove the identity
c. If the distance from A to B is no longer horizontal, but slopes up at an angle of θ, as in the diagram, find an expression for x in terms of α , β , θ and d.