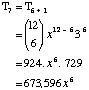This topic explains a method of expanding binomial expressions such as (x + 3)7 without having to multiply out the brackets.The Binomial Coefficients
A coefficient is the number in an algebraic term. e.g. In 7x3 the coefficient is 7.
A binomial coefficient is the coefficient of a term in a binomial expansion of the form (a + b)n
Investigation of the binomial expansions for different values of n reveals some interesting results:
|
binomial
|
binomial expansion
|
binomial coefficients
|
|
(a + b)0
|
1
|
1
|
|
(a + b)1
|
a + b
|
1 1
|
|
(a + b)2
|
a2 + 2ab + b2
|
1 2 1
|
|
(a + b)3
|
a3 + 3a2b + 3ab2 + b3
|
1 3 3 1
|
|
(a + b)4
|
a4 + 4a3b + 6a2b2 + 4ab3 + b4
|
1 4 6 4 1
|
|
(a + b)5
|
a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4+ b5
|
1 5 10 10 5 1
|
Note
- The triangle of binomial coefficients is known as Pascal's Triangle.
- Note that each value is the sum of the two above it.
- Notice also that there is always (n + 1) terms for a binomial to the n th power.
- The exponent of a decreases by 1 from left to right.
- The exponent of b increases by 1 from left to right.
The binomial coefficients can also be found from the combination formula:
For (a + b)4 the coefficients are 1, 4, 6, 4, 1 which is the same as 
.
These combinations can be looked up in the table of Binomial Coefficients.
All of this, leads to the Binomial Theorem
The Binomial Theorem
This states that:
 |
It is true for all values of a and b and at this level we use it only for n being a positive integer. {1, 2, 3...}
Example
= 1.32x5 + 5.16.3.x4 + 10.8.9.x3 + 10.4.27.x2 + 5.2.81. x + 1.243
= 32x5 + 240x4 + 720x3 + 1080x2 + 810x + 243
The General Term
Often, especially when n is large a specific term is required. e.g the seventh term.
To do this the general term is used:
 |
Note that this is the (r + 1)th term not the r th term
Example
Find the 7th term of (x + 3)12
Much easier than expanding out the bracket 12 times!
