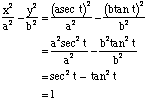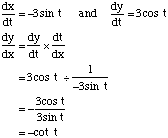BestMaths Online

The conic sections, the circle, the ellipse, the parabola and the hyperbola are not functions. The equations of the conic sections are often written as implicit relations, where y is not the subject, and this makes them difficult to deal with, especially when it comes to calculus and differentiation.

To get around this difficulty, a method called parametric equations are used. The x and y variables are each expressed in a much simpler way in terms of a third variable. t or θ are often used. These two equations are functions.

Circles

The parametric equations for the circle x² + y² = r² are:

The circle x² + y² = 9 has parametric equations x = 3cos t and y = 3sin t.

This can be checked by squaring and adding each equation.

x² = 9cos² t
y² = 9sin² t

x² + y² = 9cos² t + 9sin² t = 9(cos² t + sin² t)

x² + y² = 9

Ellipse

The parametric equations for the ellipse     are:

The ellipse     has parametric equations x = 6cos t and y = 5sin t.

Parabola

The parametric equations for the parabola y² = 4ax are:

The parabola y² = 8x has parametric equations x = 2t² and y = 4t.

This can be checked by re-arranging the equations:

and:

therefore:

Hyperbola

The parametric equations for the hyperbola 

x = a sec t y = b tan t

These can be checked by squaring and adding:

The hyperbola     has parametric equations x = 3sec t and y = 2tan t.

Parametric Equations of Translated Conic Sections

Circles, ellipses, parabolas and hyperbolas that have been translated from the centre point (0, 0) can have parametric equations too.

	Cartesian (x , y) equation	Parametric equations
Example 1 − a circle	(x − 3)2 + (y + 2)2 = 16	x = 4cos t + 3 y = 4sin t − 2
Example 2 − an ellipse		x = 5cos t − 3 y = 4sin t + 1

Differentiating Parametric Equations

One of the reasons for using parametric equations is to make the process of differentiation of the conic sections relations easier.

This concept will be illustrated with an example.

Example

A circle has the equation x² + y² = 9 which has parametric equations x = 3cos t and y = 3sin t

Using the Chain Rule: