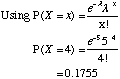The Poisson distribution describes the distribution of events which occur randomly in a continuous interval. e.g. Time, length, volume etc. The following conditions must apply:
- The events occur at random
- The events are independent of one another
- Two or more events do not occur simultaneously
- The probability that an event occurs in an interval is proportional to the size of that interval
The Poisson distribution has only one parameter and that is λ the average number of occurrences of an event in a given time interval. i.e. A rate.
Examples of Poisson Distribution
Examples of events which could follow a Poisson distribution are:
the number of cars visiting a service station in one half day.
the number of nails in a metre of wood.
the number of telephone calls arriving at a company's switchboard
Poisson Probability from Formula
The formula for Poisson probability is:
 |
for x = 0, 1, 2, 3, ... λ is the mean number of occurrences in a given time or space and can be any positive value. |
Example
The average number of cars passing a speed camera in an hour, which are exceeding the speed limit is 5.
Find the probability that in the next hour 4 cars passing the camera will be speeding.
λ = 5 and x = 4
Poisson Probability from Tables
Rather than use the formula for finding Poisson probabilities, tables are available to look these up.
A table of the Poisson Distribution for values of λ from 0.1 to 6 are given with the Bursary examination.
The part of the table for for λ = 5 and x = 4 is shown below:
|
x\λ
|
4.2
|
4.4
|
4.6
|
4.8
|
5
|
5.2
|
5.4
|
5.6
|
5.8
|
6
|
|
0
|
0.015
|
0.0123
|
0.0101
|
0.0082
|
0.0067
|
0.0055
|
0.0045
|
0.0037
|
0.003
|
0.0025
|
|
1
|
0.063
|
0.054
|
0.0462
|
0.0395
|
0.0337
|
0.0287
|
0.0244
|
0.0207
|
0.0176
|
0.0149
|
|
2
|
0.1323
|
0.1188
|
0.1063
|
0.0948
|
0.0842
|
0.0746
|
0.0659
|
0.058
|
0.0509
|
0.0446
|
|
3
|
0.1852
|
0.1743
|
0.1631
|
0.1517
|
0.1404
|
0.1293
|
0.1185
|
0.1082
|
0.0985
|
0.0892
|
|
4
|
0.1944
|
0.1917
|
0.1875
|
0.182
|
0.1755
|
0.1681
|
0.16
|
0.1515
|
0.1528
|
0.1339
|
|
5
|
0.1633
|
0.1687
|
0.1725
|
0.1747
|
0.1755
|
0.1748
|
0.1728
|
0.1697
|
0.1656
|
0.1606
|
|
6
|
0.1143
|
0.1237
|
0.1323
|
0.1398
|
0.1462
|
0.1515
|
0.1555
|
0.1584
|
0.1601
|
0.1606
|
|
7
|
0.0686
|
0.0778
|
0.0869
|
0.0959
|
0.1044
|
0.1125
|
0.12
|
0.1267
|
0.1326
|
0.1377
|
If the above question asked for the probability that there are four or fewer speeding cars i.e. P(X ≤ 4) then the probabilities for x = 0, 1, 2, 3 and 4 would need to be added together.
P(X ≤ 4) = 0.0067 + 0.0337 + 0.0842 + 0.1404 + 0.1755 = 0.4405
Mean and Variance of the Poisson Distribution
There are formulae for working the mean, variance and standard deviation of a binomial distribution.
| Mean (expected value) | μ = λ |
| Variance |
σ2 = λ |
| Standard deviation | σ = √λ |
In the example above:
E(X) = λ = 5
VAR(X) = λ = 5
SD(X) = √λ = √5 = 2.236 (to 4 sig. fig.)
Further Poisson Example
|
Cars arrive at a service station at the rate of 24 per hour. Let X represent the Poisson random variable for the number of cars arriving. a. Find the probability that 8 cars arrive in a 15 minute period. |
The probability that 8 cars arrive in 15 minutes is 0.1033 b. Find the probability that more than 3 cars arrive in a 15 minute period.
The probability that more that 3 cars arrive in 15 minutes is 0.8488 |
