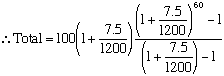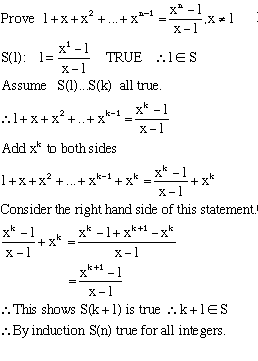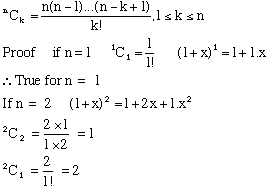BestMaths Online

Induction and the Financial Applications of Series

Review of Geometric Series

a, ar, ar², ... , ar^n-1

is a GEOMETRIC SEQUENCE where a is the first term and r is the common ratio.

When these terms are summed or added together a GEOMETRIC SERIES is obtained.

Compound Interest

A useful application of the geometric sequence is for compound interest problems.

If an initial amount of money $P is invested at a compound interest rate of r % per period and if A₁, A₂ .. A_n are the accumulated amounts at the end of each period then

A_{k + 1} = A_k + r/100. A_k = A_k(1 + r/100)

If A₀ = initial amount = P then we see that

A₁ = P(1 + r/100)

A₂ = A₁(1 + r/100) = P(1 + r/100)²

Thus deduce that :

An = P(1 + r/100)n

Examples

Example One 
$1000 is invested for two years at an annual rate of interest of 8% payable monthly.
How much is the investment worth at the end of the two years?

Here the period is a month
Therefore, n = 2 × 12 = 24
r = 8/12 = 2/3

Using the compound interest formula above
A₂₄ = 1000(1 + 2/300)²⁴

       = $1173

Example Two
Suppose I deposit $100 at the start of each month into an account earning 7.5% per annum. Interest is compounded monthly. How much will I have in the account after 5 years?

Here we track the progress of each monthly deposit.

The first $100 is invested for 60 months and earns 7.5/12 % interest per month.
Therefore, Total = 100(1 + 7.5/1200)⁶⁰ = A₁

The second amount is invested for 59 weeks
Therefore, A₂ = 100(1 + 7.5/1200)⁵⁹ etc.

Therefore, Total = A₁ + A₂ + ... A₆₀

= 100(1 + 7.5/1200)⁶⁰ + ... + 100(1 + 7.5/1200)

= 100(1 + 7.5/1200)[(1 + 7.5/1200)⁵⁹ + ... +1]

In the square brackets [     ] is a geometric series.

with a = 1 and r = (1 + 7.5/1200) and n = 60

                 = $7298

This example is typical of a superannuation fund type investment.

Time payments or Mortgages

A second application of geometric series to financial problems is in time payments ormortgages. They are also called "reducible interest loans" as interest is charged on a decreasing amount owed after each repayment.

Suppose $A is loaned to be repaid in equal instalments with an interest rate of r % per period being charged on money still owed.

Let the period repayment be $M
Let A₁, A₂ ,,, etc. be the amount still owing after each period.
Then A₁ = A(1 + r/100) − M
A₂ = A₁(1 + r/100) − M

     = A(1 + r/100)² − M(1 + r/100) − M

Deduce A_n = A(1 + r/100)ⁿ − M(1 + r/100)^{n -1} − ... M(1 + r/100) − M

But A_n = 0 since loan now repaid.

Therefore, A(1 + r/100)ⁿ = M[(1 + r/100)^n-1 + ... + (1 + r/100) + 1]

Again the [  ] contains a geometric series.

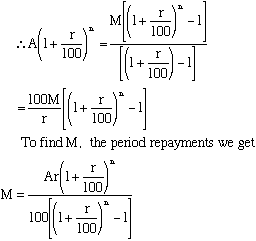
Note: Do not try to memorise this formula but work each problem following the steps of the derivation.

Example One

A $100 000 mortgage is to be repaid over 20 years in monthly instalments. The annual interest rate is 6.95% and is applied monthly.

Calculate the monthly repayments.

Here n = 20 × 12 = 240
r = 6.95/12
A = 100 000

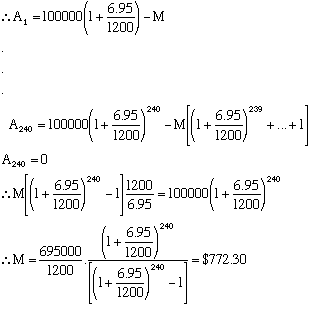
Note: This means that total repayments are 240 × $772.3 = $185352.

Thus $85352 interest is paid!!!

Example Two

In the above example how much has been repaid after 10 years?

Let us calculate A₁₂₀

= 199970 − 133306

= $66664 still owing

i.e. $33336 repaid.

---

Proofs By Induction

Suppose we have some statement S(n) depending on the positive integer n.

Let S = set of all positive integers for which S(n) is true.

Suppose we can prove the following:

(i) 1 is a member of S i.e. S(1) is true.
(ii) If all the positive integers 1, 2, ..., k are members of S then so is k+1.
i.e. S(1), S(2), ...S(k) are true then so is S(k + 1)
Then we may deduce that S(n) is true for all positive integers.

This process is called proof by induction.

Example

Prove S(n): 

Proof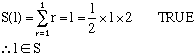     

Now assume S(1), S(2), ... S(k) are all true

specifically 

Therefore, If we add (k+1) to both sides.

1 + 2 + ...+ k + (k + 1) = 1/2.k(k + 1) + (k + 1)

Therefore, S(k +1) is true

Therefore, The proof by induction is complete and 

The proof works as follows:

If 1  S and (ii) has been proved then 1, 2  S. In turn this allows us to deduce 1, 2, 3  S and so on without limit. In most examples you only need the assumption S(k) is true to deduce S(k + 1).

Example One

Example Two Prove 7n + 2 is divisible by 3 for all positive integers. We can rewrite this as: S(n):    7n + 2 = 3m where m is an integer S(1):    71 + 2 = 9 = 3 × 3      Therefore, 1  S Assume S(k): 7k + 2 = 3m is true. Consider 7k + 1 + 2 = 7k.7 + 2 But 7k = 3m − 2 Therefore, 7k + 1 + 2 = (3m − 2)7 + 2 = 21m − 12 = 3(7m − 4) Now if m is an integer so is 7m − 4 7k + 1 + 2 = 3 × Integer Therefore, k + 1  S By induction 7n + 2 is always divisible by 3

In the theory of Binomial Expansions the coefficient of x^k in the expansion (1 + x)ⁿ is written ⁿC_k

Therefore, (1 + x)ⁿ = ⁿC₀ + ⁿC₁ x + ⁿC₂ x² + ... + ⁿC_n xⁿ

Putting x = 0 gives ⁿC₀ = 1

Also the Pascal's Triangle theorem states that:

^{n -1}C_{k -1} + ^{n -1}C_k = ⁿC_k

This, together with induction can be used to prove

Therefore, true for n = 2

Assume the formula is true for all coefficients in the expansion of (1 + x)^{n − 1}

In particular:

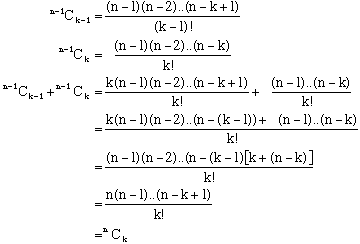
And this is known to be true by Pascal's Triangle
Therefore, If true for all coefficients in (1 + x)n also true for all coefficients in (1 + x)ⁿ
But proved for n = 1 and n = 2
Therefore, true for all positive integers.

Note:

Induction can be extended for use in proving statements based on any set with

(i) An initial value
(ii) Every member has a "next" element

e.g. S = {4, 5, 6, ...} all integers ≥ 4
S = {1/4, 1/2, 3/4, ..} all multiples of 1/4 ≥ 1/4

Induction cannot be used on sets of real numbers since a real number has no "next" element.