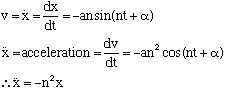A particular form of motion in a straight line where a particle oscillates about a central point is called simple harmonic motion (SHM).
Common examples are:
a. A mass moving up and down at the end of a spring or elastic string.
b. The depth of water at a point at sea varying with the tide.
c. Small oscillations of a pendulum.
O is the centre of motion
A and A1 are the extreme positions
P is the position at time t
The distance OA = OA1 = a is called the amplitude of the motion
x = acos(nt + α) is a mathematical model for the motion.
Note: We could also use asin(nt + α)
This means in a simple harmonic motion that the acceleration is directed towards O and is proportional to the distance from O, thus it can be produced by a force with this property.
Terminology
1. The angle (nt + α) is always measured in radians and is called the phase of the motion.
(Remember that π radians = 180o)
When t = 0 the phase is α,called the initial phase.
If particle starts at A then α = 0
Note: Think what α would be if the particle starts at O or A1
2. The period, T, is the time to complete one oscillation.
i.e. The phase increases by 2π
Therefore, n(t + T) + α = nt + α + 2π
|
Therefore, T = 2π / n
|
3. The frequency, f, is the number of oscillations in one second.
|
Therefore, f = 1/T = n/ 2π
|
Also note that v2 = n2x2 = a2n2 (sin2(nt + α) + cos2(nt + α))
Therefore, v2 + n2x2 = a2n2
|
Therefore, v2 = n2(a2 − x2)
|
v = 0 when x = ± a
i.e. At A1 and A as we would expect
Also vMAX = ±an at the centre O
Examples
Example 1 A particle doing simple harmonic motion has a period of 6 seconds and an amplitude of 6 cm. Find its acceleration and velocity when it is 4 cm to the left of the centre.
T = 6 = 2π/n
Therefore, n = π/3
Use v2 = n2(a2 − x2) with a = 6 and x = -4
Therefore, v2 = π2/9(36 − 16) = 20π2/9
Therefore, v = 4.68 cm/s
Acceleration = -n2x
= -π2 /9.-4 (-4 because LEFT of O)
Acceleration = 4π2/9 cm/s2
Example 2
A particle doing simple harmonic motion is initially 4 cm to the right of centre and travelling away from the centre with a velocity of 3 cm/s
The period of the motion is 8 seconds.(i) Find a and α
(ii) Find the maximum speed
(iii) Find how long it takes the particle to first reach the centre.(i) T = 2π/n = 8 Therefore, n =π/4
Use v2 = n2(a2 − x2) to find a
v = 3 when x = 4
Therefore, 9 = π2/16(a2 − 16)
Therefore, a2 = 9x16/π2 + 16
Therefore, a = 5.53 cmTherefore, x = 5.53 cos(π/4.t + α)
When t = 0 then 4 = 5.53cosα
Therefore, cosα = 0.7232
Therefore, α = ±0.762 (cosine is positive in first/fourth quadrants)
But v = -5.53π/4.sin(π/4.t + α)But v = +3 when t = 0 (Moving away from the centre)
Therefore, sinα must be negative
Therefore, α = -0.762(ii) vMAX = an = 5.53π/4 = 4.34 m/s
(iii) x = 5.53cos(π/4.t − 0.762)
If x = 0 cos(π/4.t − 0.762) = 0
Therefore, π/4.t = π/2 + 0.762Therefore, t = 2.97 seconds
