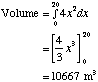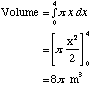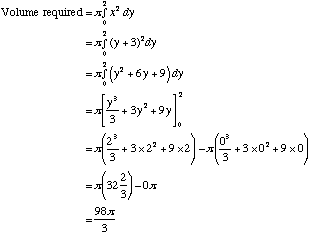Integration is useful for finding volumes, provided the object has an axis of symmetry.
Finding Volumes using Integration
The basic idea is to cut the object up into many thin slices each perpendicular to the axis of symmetry. The area of a typical slice is then found and these are then summed by integrating between the limits of the given figure. The differential, dx, represents the thickness of the slice.
| Example | ||
|
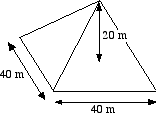
Use integration to find the volume of this square-based pyramid. The base is 40 m by 40 m. The height is 20m. |
 |
|
|
The pyramid is placed on a graph on its side. A typical slice is a square with side 2x. It has an area of 4x2 and a thickness of dx.
|
 |
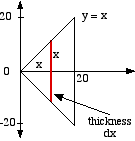A typical slice looks like this. |
Volumes of Revolution
By far the most important application of volumes and integration is finding the volume of figures with circular cross-sections.
These are obtained by rotating a curve on a graph about either the x-axis or the y-axis.
| Example | ||
|
The curve y = √ x with 0 < x < 4 is rotated about the x-axis. Find the volume of revolution. Here a typical slice is a circle, with radius √ x. The area of the slice is:
|
 |
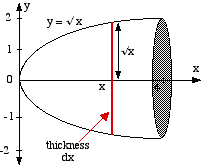A typical slice looks like this. |
In general:
|
For volumes around the x-axis:
where a and b lie on the x-axis. |
and
|
For volumes around the y-axis:
where c and d lie on the y-axis. |
Example
|
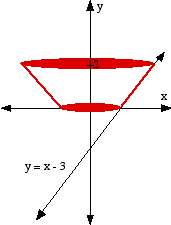
The part of the line y = x − 3 between y = 0 and y = 2 is rotated about the y-axis. Find the volume of the solid generated. .y = x − 3
|
|
