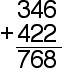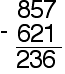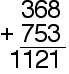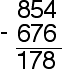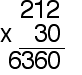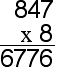|
Whole numbers can be written in normal form or expanded form.
|
Normal form
|
Expanded form
|
|
3456
|
3000 + 400 + 50 + 6
|
The position of each digit in a number shows its value.
For 3456:
|
Thousands
|
Hundreds
|
Tens
|
Units or Ones
|
|
3
|
4
|
5
|
6
|
This shows that:
3456 = 3 × 1000 + 4 × 100 + 5 × 10 + 6 × 1
|
|
Before you start using all of these different types of numbers and operations you should make sure you know your tables. Even when calculators are available, it would be useful and make your work quicker if you could add, subtract and multiply the numbers from 1 to 10 in your head.
The Four Basic Operations without a Calculator
Numbers can be added, subtracted, multiplied or divided.
Make sure you understand the following whole number calculations.
|
Adding
|
Subtracting
|
|
With no carrying, borrowing or renaming.
First add the ones (6 and 2)
Then add the tens (4 and 2)
Then add the hundreds (3 and 4)
|
example:
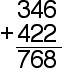
|
With no carrying, borrowing or renaming.
First subtract the ones (1 from 7)
Then subtract the tens (2 from 5)
Then subtract the hundreds (6 from 8)
|
example:
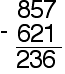
|
|
With some carrying, borrowing or renaming.
There are several methods for doing this type of addition.
|
example:
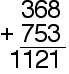
|
With some carrying, borrowing or renaming.
There are several methods for doing this type of subtraction.
|
example:
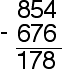
|
|
Multiplying
|
Dividing
|
|
By multiples of 10, 100 and 1000
Add the same number of zeroes.
|
example:
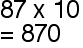
|
By multiples of 10, 100 and 1000
Remove the same number of zeroes.
|
example:
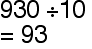
|
|
With multiples of 10, 100 and 1000
The zero is there as a place-holder.
|
example:
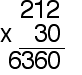
|
With multiples of 10, 100 and 1000
|
example:
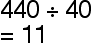
|
With some carrying, borrowing or remaning
There are several methods for doing this type of multiplication.
|
example:
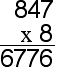
|
With some carrying, borrowing or remaning
There are several methods for doing this type of division.
|
example:
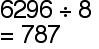
|
The Four Basic Operations with a Calculator
Some of the above examples are shown below done on a calculator.
Make sure you know how to use a calculator to do these.
Longer Calculations
You may need to do calculations involving more than two numbers:
e.g. 3 + 4 − 6 + 8 = 9
345 + 563 +165 = 1073
43 × 23 × 12 = 11868
These can be done with or without a calculator.
Divisibility
There are some useful "tricks" to help you decide whether a number is a factor of another number. This is called divisibility.
Click the numbers below to find out what they are.
Some Other Words used with Numbers
The SUM of numbers is when they are added together.
The DIFFERENCE between numbers is when they are subtracted.
The PRODUCT of numbers is when they are multiplied.
For the calculation 10 ÷ 2 = 5
10 is called the DIVIDEND
2 is called the DIVISOR
5 is called the QUOTIENT
|
Applications
|
|
a
|
A man buys 27 CDs at $23 each.
How much does he spend? |
Amount spent = $27 × 23
= $621
|
|
b
|
I owe my friend $35.
I pay back $19.
How much do I still owe my friend? |
Amount owing = $35 − $19
= $16
|
|
c
|
In a year I eat about 320 apples, 250 bananas and 190 kiwifruit.
What would be the total number of pieces of this fruit that I would eat in 5 years? |
|
Number of pieces of fruit eaten in one year
= 320 + 250 + 190
= 760 pieces of fruit
In 5 years number of pieces of fruit eaten
= 5 × 760
= 3800 pieces of fruit
|
|
d
|
I borrow $154 from my friend. I pay it back at $14 per week.
How many weeks will it take to pay it all back? |
Number of weeks = 154 ÷ 14 = 11 weeks
|
|