The decimal system is based around the number 10.
Examples of decimal numbers are 34.98 and 0.375
The part of the number in front of the dot (called the decimal point) is a whole number
The part of the number after the dot is a decimal fraction.
![]()
A number can be written in decimal form e.g. 4.25
OR it can be written in expanded form i.e. 4 + 2⁄10 + 5⁄100
Types of Decimals
- A terminating decimal is one that has a finite number of digits.
- e.g. 0.5 and 0.875
- A recurring or repeating decimal is one that has a repeating sequence of digits. Recurring decimals are shown by a dot above the recurring digits or at the beginning and end of the repeatingsequence.
e.g.
0.3333... 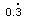
0.1666... 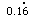
0.207207... 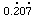
All fractions can be represented by terminating or recurring decimals.
- A non-repeating decimal is a decimal that contains a non-repeating sequence of decimal digits.
- e.g. 0.810675469... does not repeat.
When an answer works out to a large number of decimal places or the answer does not need to be given so accurately it can be rounded.
e.g. 4 ÷ 7 = 0.5714285714... goes on forever!
This number can be rounded to a certain number of decimal places.
| e.g. 0.5714285714 can be rounded to : |
0.6
|
0.57
|
0.571
|
0.5714
|
•If this number is below 5 (that is 0,1, 2, 3 or 4) then the 3 decimal place number stays the same.
•If this number is equal to, or above 5 (that is 5, 6, 7, 8 or 9) then ADD one to the 3 decimal place number. e.g. 2.3585 becomes 2.359 when rounded to 3 decimal places. |
Operations
Calculators can be used to carry out the following operations involving decimals.
However, it is useful to be able to do these basic operations without a calculator.
Adding and subtracting
Make sure that the decimal points are in line.
|
Calculate: |
|
|
(a) 4.5 + 3.62 |
|
|
(b) 2.34 − 0.73 |
Multiplying
- To multiply by multiples of 10, move the decimal point to the right.
- When multiplying two decimal numbers, carry out the calculation ignoring the decimal points. Place the decimal point in the answer so that the answer has the same number of decimal places as the total number of places in the two numbers being multiplied.
|
Calculate: |
|
|
(a) 0.27 × 100 |
(a) |
|
(b) 3.4 × 1000 |
(b) |
|
(c) 0.4 x 0.5 |
(c) 0.4 x 0.5 = 0.20 |
|
(d) 3.6 x 6 |
(d) 3.6 x 6 = 21.6 |
|
(e) 1.3 x 1.2 |
(e) 1.3 x 1.2 = 1.56 |
Division
- When dividing by multiples of 10, move the decimal point to the left.
- When dividing two decimal numbers, write the calculation as a fraction.
Move the decimal point in both the numerator and the denominator the same number of decimal places needed to make the bottom line into a whole number. Then carry out normal division.
|
Calculate: |
|
|
(a) 16.5 ÷ 10 |
(a) |
|
(b) 152 ÷ 100 |
(b) |
|
(c) 31.5 ÷ 5 |
(c) |
|
(d) 34.56 ÷ 0.4 |
(d) |