Pythagoras' Theorem links the lengths of sides of right angled-triangles.
This section of trigonometry makes connections between the lengths of sides and angles in right-angled triangles.
Right-angled Triangles
|
Given a right-angled triangle with an angle marked a as shown: In the diagram:
Greek letters, such as α are often used in trigonometry. |
 |
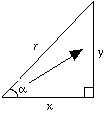There are several methods used for finding angles and sides in right-angled triangles. You may have been taught and use a different one to that shown below. They all produce the same answers if done correctly!
For example, some people call the opposite side, the separated side and the adjacent side, the connected side.
|
In the triangle shown, how long is: (a) The side opposite to θ ? (b) The side adjacent to θ ? (c) The hypotenuse? |
 |
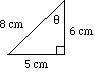(a) The opposite side is 5 cm long. (b) The adjacent side is 6 cm long. (c) The hypotenuse is 8 cm long.
|
Trigonometric Ratios
For a right-angled triangle: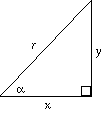
|
Sine of angle α = |
|
|
|
Cosine of angle α = |
|
|
|
Tangent of angle α = |
|
TOA |
Circular Functions
The trigonometric ratios are also known as circular functions and the sine, cosine and tangent of any angle, positive or negative can be found.
Click here for an activity showing the sine as a circular function.
Click here for an activity showing the cosine as a circular function.
Click here for an activity showing the tangent as a circular function.
Finding Ratios
The sine, cosine and tangent ratios are the same for a particular angle regardless of the size of the triangle.
The ratios can be found using a calculator or from a book of trigonometric tables.
Calculators.
Most calculators have trigonometric function keys. These will give the sine, cosine, and tangent of an angle as well as the inverse of these functions. These decimals will be given to a large number of significant figures, which will often need to be rounded off (4 significant figures is usually accurate enough).
e.g To find sine 53° press 
0.798635510 which could then be rounded as necessary.
The other trigonometric buttons are 
and 
.
Care must be taken to ensure that the calculator is set to work in values in degrees (DEG), as there are other ways of measuring angles such as radians (RAD) and gradians (GRAD). Use the mode button to change these settings.
Tables.
Before the days of calculators, everyone used printed tables giving the trigonometric ratios and these can be used if you do not have a calculator available. These tables give the ratios for angles from 0° to 90° to four or five significant figures, with angles being given to 1 decimal place.
