Year 12 Quiz

Question 1. Find the mean, median and mode for the following data:
2, 3, 31, 5, 6, 19, 5

The mean is the common average. The mode is the most common.The median is the middle value.

Mean = 10.1 (to 3 sig. fig.) Mode = 5 Median = 5

Question 2. Write f(x) = x² - 4x + 11 in the form
f(x) = (x − a)² + b

Complete the square

f(x) = (x − 2)² + 7

Question 3. For the graph of the equation x²/3 + y²/9 = 1
What are the x intercepts?

Put y = 0 into the equation

(+√3, 0) and (−√3, 0)

Question 4. Solve the equation sin2x = 0.5
for 0° ≤ x ≤ 360°

There are 4 solutions. (use the graph of y = sin2x)

15°, 75°, 195°, and 255°

Question 5. A school contains 500 students. What is the probability that a student chosen at random is born on the first day of a month?

How many first days of a month are there?

12/365

Question 6. What is the minimum value of x² − 4x + 11?

Complete the square

x² − 4x + 11 = (x − 2)² + 7
So the minimum value is 7

Question 7. Solve |x + 4| < 1

|x + 4| < 1 means
−1 < x + 4 < 1

−5 < x < −3

Question 8. Find f '(x) if f(x) = 3x² - 2/x

Write 2/x as 2x^-1 then differentiate

f' '(x) = 6x + 2x⁻²
= 6x + 2/x²

Question 9. If f(x) = x³ - 2x² + 3x + 1
find f(-1)

Substitute x = -1 into f(x)

f(-1) = (-1)³ - 2 x (-1)² + 3(-1) + 1
= -1 - 2 - 3 +1
= -5

Question 10. For the graph of x²/3 + y²/9 = 1 what are the y-intercepts?

Put x = 0

(0, 3) and (0, -3)

Question 11. Expand 2(3 - x)²

Expand first and then multiply by 2

y = 18 - 12x + 2x²

Question 12. Find the median and the interquartile range of
2, 3, 5, 19, 5, 31, 6

Median is the middle value and the interquartile range is the difference between the upper quartile and the lower quartile

Median is 5 and the interquartile range is
19 - 3 = 16

Question 13. Simplify √(x⁵) . √(x³)

Write roots as indices and then ADD them.

x^5/2 . x^3/2 = x⁴

Question 14. Solve sinA = 0.188 for 0° ≤ A ≤ 180°
(Give answer in degrees to 1 decimal place)

Use sin^-1 on calculator. There are 2 solutions.

10.8° and 169.2°

Question 15. R and Q are two independent events with P(R) = 0.4 and P(Q) = 0.3
What is P(R U Q)?

P(A U B) = P(A) + P(B) - P(A n B)

P(R U Q) = 0.4 + 0.3 - 0.4 x 0.3
= 0.7 - 0.12 = 0.58

Question 16. Find the median for:
36, 42, 41, 39, 32, 49, 28, 56

Arrange in order first.

The median is 40

Question 17. Find f '(x) if f(x) = tan(x³)

Use the differentiation formula

f ' (x) = 3x².sec²(x³)

Question 18. Simplify (a² x an) / a^{n + 2}

The Laws of Indices must be used.

1

Question 19. If g(x) = 2x³ + 3x² - 12x + 3, find g''(x)

g'' means differentiate TWICE

g''(x) = 12x + 6

Question 20. Solve log₅x = 1

use the Properties of Logarithms

x = 5

Question 21. Evaluate ⁷C₄

Look up the COMBINATION formula or use your calculator

⁷C₄ = 35

Question 22. What type of graph is given by the equation y = 4√x?

It is one of the conic sections.

It is the equation of part of a parabola.

Question 23. Evaluate log₅5

Use the properties of logarithms

log₅5 = 1

Question 24. Find ʃ3 + e^3x dx

Differentiate term by term

f'(x) = 6x² − 6x + 4

Question 25. What are the coordinates of the points of intersection of the graphs of y = x2 and y = 1?

Substitute y = 1 into y = x²

(1, 1) and (-1, 1)

Question 26. What are the parametric equations of the conic
x²/49 - y²/100 = 1

Use x = a secθ and y = b tanθ

x = 7secθ
y = 10tanθ

Question 27.Find the sample standard deivation for:
36, 42, 41, 39, 32, 49, 28, 56

Use the σ_{n - 1} button on your calculator.

The sample standard deviation is 8.99

Question 28. Find f '(x) if f(x) = 3(x - 2)⁵

Use the function of a function (composite function) rule.

f' (x) = 15(x - 2)⁴

Question 29. When a²/√ a is written in the form aⁿ.
What is n?

For the division of terms, SUBTRACT the exponents.

n = 3/2

Question 30. Find the midpoint of the line joining the points (1, -3) and (-1, 5)

Use the midpoint of a line theorem.

(0, 1)

Solve tanC = 2.85
(Give answer in radians to 3 significant figures.)

Use "shift" and "tan" on your calculator.

C = 1.23

Question 32. Simplify (x² - x - 6)/(x² - 9)

Factorise the numerator

(x + 2)/(x + 3)

Question 33. What type of graph is given by the equation x²/3 + y²/9 = 1 ?

It is one of the conic sections.

It is an ellipse

Question 34. What are the coordinates of the centre of the circle given by the equation x² + y² - 2x - 4y - 9 = 0?

Complete the square for x² - 2x and y² - 4y

The centre of the circle is (1, 2)

Question 35. The random variable X has the following probability distribution. Find P(X = 7)

The sum of the probabilities is ONE.

P(X = 7) = 0.1

Question 36. Differentiate 4x³ + 2e^2x

Differentiate term by term.

f '(x) = 12x² + 4e^2x

Question 37.Find e^4.2 correct to 2 decimal places.

Use calculator

66.69

Question 38. Evaluate cos2x if sinx = 1/16

Use a double angle formula

cos2x = 127/128

Question 39. For the equation y = (2x - 3)/(x + 2)
What is the equation of the horizontal asymptote?

Try dividing out the rational fraction.
(sometimes known as the cover-up rule)

y = 2

Question 40. What is the integral of 3/x ?

The integral of 1/x is ln x

3ln x

Question 41.Find the standard deviation of 2, 3, 31, 5, 6, 19, 5

Use the statistics function of your calculator.

Standard deviation = 10.01

Question 42. Solve 3cosC = 0.625 for 0 ≤ C ≤ 180°

Divide both sides by 3

C = 78.0°

Question 43. What is the minimum value of the function
f(x) = x² + 4x + 7?

Complete the square on x² + 4x

The minimum value of the function is 3

Question 44. What is the upper quartile of 36, 42, 41, 39, 32, 49, 28, 56?

Arrange the numbers in order first.

The upper quartile is 45.5

Question 45.Solve x² - 4x = 8
Leave answer in surd form ( with square roots)

Complete the square

x = 2 ± √12

Question 46. Differentiate x³(2x + 3)

Expand the brackets first - easiest (unless you use the product rule)

f '(x) = 8x³ + 9x²

Question 47. W Simplify 12b¹² ÷ (2b³)²

Laws of Indices! Remember to square the 2 in the brackets.

3b⁶

Question 48. Find the points on the line joining (1, -3) and (-1, 5) which divides it internally in the ratio 2:1

Look up the formula! A diagram may help to check your answer.

(-1/3, 7/3) or (1/3, -1/3)

Question 49. Make y the subject of the formula x = (3y + 2)/(y - 1)

The first step is to multiply both sides by (y - 1) Then get all of the x terms to one side and all of the y terms to the other.

y = (2 + x)/(x - 3)

Question 50. Find ʃ(3x² + 2/x) dx

Integrate term by term and don't forget the "c"!

x³ + 2ln |x| + c

Question 51.If an experiment has events R and S with P(R) = 0.3
Find P(R')

P(R') is the probability that event R does NOT happen.

P(R') = 1 - 0.3 = 0.7

Question 52. if e^3x = 4.8 find x to 2 significant figures.

Take natural logarithms of both sides.

x = 0.52 (to 2 s.f.)

Question 53. Evaluate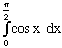

Integrate cos x first and then substitute the values.

1

Question 54. Write sin5x - sinx as a product.

Use the sum to product formula

2cos3x sin2x

Question 55. Suppose that Q and R are events with
P(Q) = 0.25, P(R) = 0.4 and P(QnR) = 0.12. Are Q and R independent events? Give a reason for your answer.

Is P(Q) x P(R) = P(QnR)?

P(Q) x P(R) = 0.25 x 0.4 = 0.1
which is NOT equal to 0.12. Therefore the events are NOT independent.

Question 56. Is the region given by the inequality 3y < 10 - 2x above the line or below it?

Sketch the line 3y = 10 - 2x and then "test" the inequality with the point (0, 0)

The required region is BELOW the line

Question 57. Find the coordinates of the point of intersection of the simultaneous equations
2y - x = 20, x + y = 100
You should be able to do this one in your head!

The elimination method is probably the easiest method to find the point. (Just add the two equations)

The point of intersection is (60, 40)

Question 58. Solve 3.1^x = 81 (to 3 significant figures)

Take logarithms to base e of both sides.

x = 3.88

Question 59. If X and Y are independent random variables with E(X) = 7, E(Y) = 9, VAR(X) = 3 and VAR(Y) = 2.
Find the mean value of the random variable 4X - Y

E(aX + bY) = aE(X) + bE(Y)

E(4X - Y) = 4 x 7 - 9 = 19

Question 60. What is the equation of the horizontal asymptote of the hyperbola given by the equation
f(x) = 3/(x - 2)?

What happens to the value of the function, as x gets larger?

y = 0 (the x-axis) is the horizontal asymptote.

Question 61.Find x given that log_ex² + log_ex = 9 (Give answer to 1 decimal place.)

Use the properties of logarithms

x = 20.1

Question 62. If f(x) = 1/x³ find f '(x)

Write 1/x³ in index form

f '(x) = -3/x⁴

Question 63. Simplify (x² - 2x - 3)/(x + 1)

Factorise the numerator first and then cancel

x - 3

Question 64. Find ∫ (x − 3)(3x + 2) dx?

Expand the brackets first.

x³ − 3.5x² − 6x + c

Question 65. Write log³81 = 4 as an exponential statement.

It will be in the form a^b = c

3⁴ = 81

Question 66.If X and Y are independent random variables with E(X) = 7, E(Y) = 9, VAR(X) = 3 and VAR(Y) = 2.
Find the variance of 5X + 2Y

VAR(aX + bY) = a²VAR(X) + b²VAR(Y)

VAR(5X + 2Y) = 5² x 3 + 2² x 2 = 83

Question 67. Find x, in radians, to 3 significant figures, such that sinx = -0.3
for 0 ≤ x ≤ 2π

Use the calculator to find one of the solutions and then use the graph of y = sin x and symmetry to find the ones in the domain given.

x = 3.45 and 5.98

Question 68. Find x given that log_bx³ = 3

Use properties of logarithms.

x = b

Question 69. Find x in radians such that cos x = -0.3 for 0 ≤ x ≤ 2π
Give answers to 3 significant figures.

Use calculator to find one value and then use the graph of y = cos x and its symmetry to find the required values.

x = 1.88 and 4.41

Question 70. Solve 5(x - 2) = 5x - 10

How many possible solutions are there?

There are an infinite number of solutions so x € R

Question 71. Find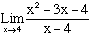

Factorise then simplify then substitute.

5

Question 72. Use the statistical mode of your calculator to find the mean of
3.4, 5.6, 8.9 and 4.9?

Most calculators show SD on the display when in statistical mode. Make sure you clear any existing statistical data.

mean = 5.7

Question 73. What is the maximum value of the function y = -2x² + 1?

Think of the shape of the graph. What effect does the +1 have on the function?

The maximum value is 1

Question 74. Use the statistical mode of your calculator to find the standard deviation of 3.4, 5.6, 8.9 and 4.9

Most calculators show the statistical mode with SD on the display. Be sure to clear any stored data from the calculator before starting..

SD = 2.01 (to 3 s.f.)

Question 75. If g(x) = 2x² - 3x, calculate the rate of change of g(x) when x = 1

Differentiate to find the rate of change and then substitute x = 1

g '(x) = 4x - 3
When x = 1
g' (1) = 1

Question 76. Differentiate
cos 5x sin 3x

Question 77. Find the 25th term of the sequence 3, 7, 11, ...

Use the formula
^tn = a + (n - 1)d

t_{25_{= 99}}

Question 78. A circle has equation x² + y² - 2x - 4y - 9 = 0 What is its radius?

Complete the square on x² - 2x and y² - 4y

The radius is 2

Question 79.State whether the sequence 3, 4, 16/3, ... is arithmetic, geometric or neither

Test to see if it has a common ratio or a common difference.

It is a geometric sequence with a common ratio of 4/3

Question 80. Differentiate 2x³ + e^2x

Differentiate term by term

6x² + 2e^2x

Question 81. A die is tossed. For the two events A and B where A is getting an odd number and B is getting a number more than 3, what is the probability of A OR B?

The word OR indicates the need to ADD the probabilities but don't count the overlap (the 5) twice

P(A OR B) = 5/6

Question 82. Find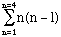

Substitute n = 1 then n = 2, then n = 3 and finally n = 4 and ADD the resultsof each together to find the SUM.

Sum = 20

Question 83. Solve the equation sin2x = -0.5 for 0 < x < 2π

Use calculator and the graph of y = sin2x

7π/12, 11π/12, 19π/12, 23π/12

Question 84. For the graph of x²/3 + y²/9 = 1, what are the y-intercepts?

Put x = 0

The y-intercepts are (0, ± 3)

Question 85. Find the mean of the following frequency distribution.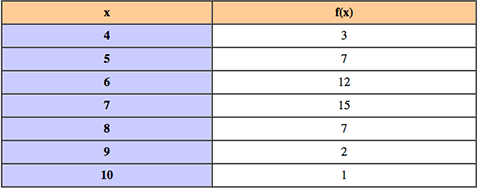

Mean = Σ(f(x). x) /Σ f(x)

Mean = 308/47 = 6.6 (to 2 s.f.)

Question 86. Evaluate ⁹P₃

Use tables, calculator of formula. Just find it!

504

Question 87.The function x²/a² + y²/b² = 1 intersects the x-axis at (4, 0) and (-4, 0), what is the value of a²?

Put y = 0

a² = 16

Question 88.How many ways are there of selecting a captain and a vice-captain from a team of 6 players?

(How many ways of picking the captian?) x (How many ways of picking the vice captain?)

There are 6 x 5 ways. i.e 30 ways

Question 89. The random variable X has the following probability distribution. What is the variance of X?

VAR(X) = E(X²) - [E(X)]²

VAR(X) = 2.44

Question 90. Find the distance between the points (1, -3) and (-1, 5)

Use the formula or draw a diagram and use Pythagoras' theorem.

Distance = √68

Question 91. What is the equation of the vertical asymptote of the rectangular hyperbola (x − 2)y + 3) = 9?

Solve the equation y + 3 = 0 or
Solve the equation x − 2 = 0
Which one?

The vertical asymptote is x = 2

Question 92. Solve cos(x + π/6) = √3/2
for 0 ≤ x ≤ 2π

Use "special" triangles or calculator. There are 3 answers in the domain given.

0, 5π/3, 2π

Question 93. If y = 5(x − 4)² What is y'?

Expand the brackets first.

y ' = 10x - 40

Question 94. If y = 5(x - 4)² What is y' ?

Expand the brackets first or use the composite function rule.

y ' = 10x - 40

Question 95.What is the equation of the vertical asymptote of the function f(x) = 3/(x - 2)?

To find the vertical asymptote of a hyperbola find the value of x that makes the denominator equal to 0

x = 2 is the equation of the vertical asymptote.

Question 96. What is the y-intercept of the graph of the graph of
y = sin(x - π/6) ?

Put x = 0 in the equation

y = -0.5

Question 97. Find ʃ 3x(x - 2)3 dx

Use the substitution u = x - 2

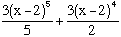Don't forget to add "+c"

Question 98. The graph of y = (3x - 4)/(2x + 1) has a vertical asymptote. What is its equation?

The vertical asymptote occurs when the denominator would be 0!

The vertical asymptote is x = -0.5

Question 99. If y = e^6x, find y

Remember: If y = e^x then y'= e^x

y' = 6e^6x

Question 100. What are the coordinates of the y-intercept of the function
f(x) = 2x³ + 3x² + 4x - 5?

Put x = 0 into the function.i.e. Find f(0)

(0, -5)

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100

Year 12 (NZ Y13) Quiz

Click on the question you wish to answer, in any order:

Red questions are about ALEGEBRA AND EQUATIONS

Blue questions are about STATISTICS AND PROBABILITY

Green questions are about GEOMETRY AND GRAPHS

Orange questions are about CALCULUS

Purple questions are about TRIGONOMETRY

Question 1. Find the mean, median and mode for the following data:2, 3, 31, 5, 6, 19, 5

Question 2. Write f(x) = x2 - 4x + 11 in the form f(x) = (x − a)2 + b

Question 3. For the graph of the equation x2/3 + y2/9 = 1 What are the x intercepts?

Question 4. Solve the equation sin2x = 0.5 for 0° ≤ x ≤ 360°

Question 5. A school contains 500 students. What is the probability that a student chosen at random is born on the first day of a month?

Question 6. What is the minimum value of x2 − 4x + 11?

Question 7. Solve |x + 4| < 1

Question 8. Find f '(x) if f(x) = 3x2 - 2/x

Question 9. If f(x) = x3 - 2x2 + 3x + 1find f(-1)

Question 10. For the graph of x2/3 + y2/9 = 1 what are the y-intercepts?

Question 11. Expand 2(3 - x)2

Question 12. Find the median and the interquartile range of 2, 3, 5, 19, 5, 31, 6

Question 13. Simplify √(x5) . √(x3)

Question 14. Solve sinA = 0.188 for 0° ≤ A ≤ 180° (Give answer in degrees to 1 decimal place)

Question 15. R and Q are two independent events with P(R) = 0.4 and P(Q) = 0.3 What is P(R U Q)?

Question 16. Find the median for: 36, 42, 41, 39, 32, 49, 28, 56

Question 17. Find f '(x) if f(x) = tan(x3)

Question 18. Simplify (a2 x an) / an + 2

Question 19. If g(x) = 2x3 + 3x2 - 12x + 3, find g''(x)

Question 20. Solve log5x = 1

Question 21. Evaluate 7C4

Question 22. What type of graph is given by the equation y = 4√x?

Question 23. Evaluate log55

Question 24. Find ʃ3 + e3x dx

Question 25. What are the coordinates of the points of intersection of the graphs of y = x2 and y = 1?

Question 26. What are the parametric equations of the conic x2/49 - y2/100 = 1

Question 27.Find the sample standard deivation for: 36, 42, 41, 39, 32, 49, 28, 56

Question 28. Find f '(x) if f(x) = 3(x - 2)5

Question 29. When a2/√ a is written in the form an. What is n?

Question 30. Find the midpoint of the line joining the points (1, -3) and (-1, 5)

Solve tanC = 2.85(Give answer in radians to 3 significant figures.)

Question 32. Simplify (x2 - x - 6)/(x2 - 9)

Question 33. What type of graph is given by the equation x2/3 + y2/9 = 1 ?

Question 34. What are the coordinates of the centre of the circle given by the equation x2 + y2 - 2x - 4y - 9 = 0?

Question 35. The random variable X has the following probability distribution. Find P(X = 7)

Question 36. Differentiate 4x3 + 2e2x

Question 37.Find e4.2 correct to 2 decimal places.

Question 38. Evaluate cos2x if sinx = 1/16

Question 39. For the equation y = (2x - 3)/(x + 2) What is the equation of the horizontal asymptote?

Question 40. What is the integral of 3/x ?

Question 41.Find the standard deviation of 2, 3, 31, 5, 6, 19, 5

Question 42. Solve 3cosC = 0.625 for 0 ≤ C ≤ 180°

Question 43. What is the minimum value of the function f(x) = x2 + 4x + 7?

Question 44. What is the upper quartile of 36, 42, 41, 39, 32, 49, 28, 56?

Question 45.Solve x2 - 4x = 8 Leave answer in surd form ( with square roots)

Question 46. Differentiate x3(2x + 3)

Question 47. W Simplify 12b12 ÷ (2b3)2

Question 48. Find the points on the line joining (1, -3) and (-1, 5) which divides it internally in the ratio 2:1

Question 49. Make y the subject of the formula x = (3y + 2)/(y - 1)

Question 50. Find ʃ(3x2 + 2/x) dx

Question 51.If an experiment has events R and S with P(R) = 0.3 Find P(R')

Question 52. if e3x = 4.8 find x to 2 significant figures.

Question 53. Evaluate

Question 54. Write sin5x - sinx as a product.

Question 55. Suppose that Q and R are events with P(Q) = 0.25, P(R) = 0.4 and P(QnR) = 0.12. Are Q and R independent events? Give a reason for your answer.

Question 56. Is the region given by the inequality 3y < 10 - 2x above the line or below it?

Question 57. Find the coordinates of the point of intersection of the simultaneous equations 2y - x = 20, x + y = 100 You should be able to do this one in your head!

Question 58. Solve 3.1x = 81 (to 3 significant figures)

Question 59. If X and Y are independent random variables with E(X) = 7, E(Y) = 9, VAR(X) = 3 and VAR(Y) = 2. Find the mean value of the random variable 4X - Y

Question 60. What is the equation of the horizontal asymptote of the hyperbola given by the equation f(x) = 3/(x - 2)?

Question 61.Find x given that logex2 + logex = 9 (Give answer to 1 decimal place.)

Question 62. If f(x) = 1/x3 find f '(x)

Question 63. Simplify (x2 - 2x - 3)/(x + 1)

Question 64. Find ∫ (x − 3)(3x + 2) dx?

Question 65. Write log381 = 4 as an exponential statement.

Question 66.If X and Y are independent random variables with E(X) = 7, E(Y) = 9, VAR(X) = 3 and VAR(Y) = 2. Find the variance of 5X + 2Y

Question 67. Find x, in radians, to 3 significant figures, such that sinx = -0.3 for 0 ≤ x ≤ 2π

Question 68. Find x given that logbx3 = 3

Question 69. Find x in radians such that cos x = -0.3 for 0 ≤ x ≤ 2π Give answers to 3 significant figures.

Question 70. Solve 5(x - 2) = 5x - 10

Question 71. Find

Question 72. Use the statistical mode of your calculator to find the mean of 3.4, 5.6, 8.9 and 4.9?

Question 73. What is the maximum value of the function y = -2x2 + 1?

Question 1. Find the mean, median and mode for the following data:
2, 3, 31, 5, 6, 19, 5

Question 2. Write f(x) = x² - 4x + 11 in the form
f(x) = (x − a)² + b

Question 3. For the graph of the equation x²/3 + y²/9 = 1
What are the x intercepts?

Question 4. Solve the equation sin2x = 0.5
for 0° ≤ x ≤ 360°

Question 6. What is the minimum value of x² − 4x + 11?

Question 8. Find f '(x) if f(x) = 3x² - 2/x

Question 9. If f(x) = x³ - 2x² + 3x + 1
find f(-1)

Question 10. For the graph of x²/3 + y²/9 = 1 what are the y-intercepts?

Question 11. Expand 2(3 - x)²

Question 12. Find the median and the interquartile range of
2, 3, 5, 19, 5, 31, 6

Question 13. Simplify √(x⁵) . √(x³)

Question 14. Solve sinA = 0.188 for 0° ≤ A ≤ 180°
(Give answer in degrees to 1 decimal place)

Question 15. R and Q are two independent events with P(R) = 0.4 and P(Q) = 0.3
What is P(R U Q)?

Question 16. Find the median for:
36, 42, 41, 39, 32, 49, 28, 56

Question 17. Find f '(x) if f(x) = tan(x³)

Question 18. Simplify (a² x an) / a^{n + 2}

Question 19. If g(x) = 2x³ + 3x² - 12x + 3, find g''(x)

Question 20. Solve log₅x = 1

Question 21. Evaluate ⁷C₄

Question 23. Evaluate log₅5

Question 24. Find ʃ3 + e^3x dx

Question 26. What are the parametric equations of the conic
x²/49 - y²/100 = 1

Question 27.Find the sample standard deivation for:
36, 42, 41, 39, 32, 49, 28, 56

Question 28. Find f '(x) if f(x) = 3(x - 2)⁵

Question 29. When a²/√ a is written in the form aⁿ.
What is n?

Solve tanC = 2.85
(Give answer in radians to 3 significant figures.)

Question 32. Simplify (x² - x - 6)/(x² - 9)

Question 33. What type of graph is given by the equation x²/3 + y²/9 = 1 ?

Question 34. What are the coordinates of the centre of the circle given by the equation x² + y² - 2x - 4y - 9 = 0?

Question 36. Differentiate 4x³ + 2e^2x

Question 37.Find e^4.2 correct to 2 decimal places.

Question 39. For the equation y = (2x - 3)/(x + 2)
What is the equation of the horizontal asymptote?

Question 43. What is the minimum value of the function
f(x) = x² + 4x + 7?

Question 45.Solve x² - 4x = 8
Leave answer in surd form ( with square roots)

Question 46. Differentiate x³(2x + 3)

Question 47. W Simplify 12b¹² ÷ (2b³)²

Question 50. Find ʃ(3x² + 2/x) dx

Question 51.If an experiment has events R and S with P(R) = 0.3
Find P(R')

Question 52. if e^3x = 4.8 find x to 2 significant figures.

Question 55. Suppose that Q and R are events with
P(Q) = 0.25, P(R) = 0.4 and P(QnR) = 0.12. Are Q and R independent events? Give a reason for your answer.

Question 57. Find the coordinates of the point of intersection of the simultaneous equations
2y - x = 20, x + y = 100
You should be able to do this one in your head!

Question 58. Solve 3.1^x = 81 (to 3 significant figures)

Question 59. If X and Y are independent random variables with E(X) = 7, E(Y) = 9, VAR(X) = 3 and VAR(Y) = 2.
Find the mean value of the random variable 4X - Y

Question 60. What is the equation of the horizontal asymptote of the hyperbola given by the equation
f(x) = 3/(x - 2)?

Question 61.Find x given that log_ex² + log_ex = 9 (Give answer to 1 decimal place.)

Question 62. If f(x) = 1/x³ find f '(x)

Question 63. Simplify (x² - 2x - 3)/(x + 1)

Question 65. Write log³81 = 4 as an exponential statement.

Question 66.If X and Y are independent random variables with E(X) = 7, E(Y) = 9, VAR(X) = 3 and VAR(Y) = 2.
Find the variance of 5X + 2Y

Question 67. Find x, in radians, to 3 significant figures, such that sinx = -0.3
for 0 ≤ x ≤ 2π

Question 68. Find x given that log_bx³ = 3

Question 69. Find x in radians such that cos x = -0.3 for 0 ≤ x ≤ 2π
Give answers to 3 significant figures.

Question 72. Use the statistical mode of your calculator to find the mean of
3.4, 5.6, 8.9 and 4.9?

Question 73. What is the maximum value of the function y = -2x² + 1?

Question 75. If g(x) = 2x² - 3x, calculate the rate of change of g(x) when x = 1

Question 76. Differentiate
cos 5x sin 3x

Question 78. A circle has equation x² + y² - 2x - 4y - 9 = 0 What is its radius?

Question 80. Differentiate 2x³ + e^2x

Question 84. For the graph of x²/3 + y²/9 = 1, what are the y-intercepts?

Question 86. Evaluate ⁹P₃

Question 87.The function x²/a² + y²/b² = 1 intersects the x-axis at (4, 0) and (-4, 0), what is the value of a²?

Question 92. Solve cos(x + π/6) = √3/2
for 0 ≤ x ≤ 2π

Question 93. If y = 5(x − 4)² What is y'?

Question 94. If y = 5(x - 4)² What is y' ?

Question 96. What is the y-intercept of the graph of the graph of
y = sin(x - π/6) ?

Question 99. If y = e^6x, find y

Question 100. What are the coordinates of the y-intercept of the function
f(x) = 2x³ + 3x² + 4x - 5?