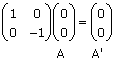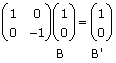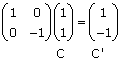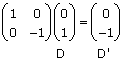Matrix multiplication can be used to transform points in a plane.
Transformations can be represented by 2 X 2 matrices, and ordered pairs (coordinates) can be represented by 2 X 1 matrices.
Transforming a point
To transform a point (x, y) by a transformation matrix 
, multiply the two matrices together.
(Transformation matrix) x (point matrix) = image point
To find out which transformation a matrix represents, it is useful to use the unit square.
The unit square is a square with vertices (0, 0), (1, 0), (1, 1) and (0, 1).
The unit square is drawn and the image of each vertex of the square is calculated by matrix multiplication. The image points are then drawn on the diagram.
The type of transformation can then be seen on the diagram.
|
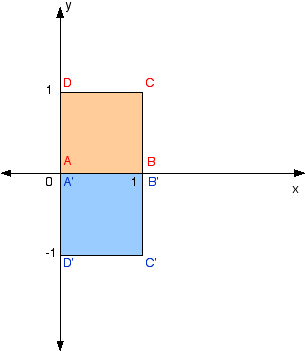
Example Use the unit square to describe the transformation given by Multiply each point of the unit square:
|
Diagram
From the diagram it can be seen that the unit square has been reflected in the x-axis. Note that the origin (0, 0) always remains invariant (unchanged) under a |
.
To save time, the vertices of the unit square can be put into one 2 x 4 matrix.
e.g.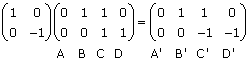 
Click here for another way of identifying transformation matrics.
Types of Transformation Matrices
Reflections and Rotations
The more common reflections in the axes and the rotations of a quarter turn, a half turn and a three-quarter turn can all be represented by matrices with elements from the set {-1, 0 , 1}.
e.g. 
represents a rotation of 180o (a half turn).
Enlargements
The general matrix for an enlargement is 
.
Where k is the scale factor for length and k 2 is the scale factor for area.
e.g. 
represents an enlargement, centre (0, 0) of scale factor 3.
Shears
The general matrix for a shear parallel to:
the x-axis is: 
the y-axis is: 
where a is the shear factor.
Translations
These can be represented by a vector. e.g. a 2 X 1 matrix
Singular Matrix
A matrix with a determinant of zero maps all points to a straight line.
Inverse Matrix
The inverse of a matrix will map an image point or shape back to its original position.
Determinant
The determinant of a transformation matrix gives the scale factor for area.
e.g. If E is a transformation matrix, |E| is the scale factor for area.
