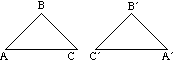Definitions for all Transformations
Invariant:A point or a set of points are invariant under a transformation if it remains unchanged by the transformation.
Isometry: An isometry is a transformation where the size and shape of an image remain the same as the object. The object and the image are congruent.
Indirect (or opposite): An indirect transformation is one in which the sense or direction of the image is changed.
Reflection
e.g. If 
ABC maps to A´B´C´ under a transformation N.
|
Angle size and length are invariant. Transformation N is an isometry. N is an indirect transformation.
|
|
A reflection is defined if the position of the mirror line or the position of a point and its image are known.The mirror line is the line at right angles to the line joining a point and its image.
Notation
M is a reflection in mirror line m.
M: A 
A´ or M(A) = A´
means A maps to A´ or A´ is the image of A.
Properties of Reflection
Triangle PQR maps to triangle P´Q´R´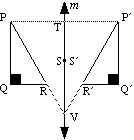 
The object is the same distance in front of the mirror line m as the image is behind it. i.e. PT = P´ T
Length, angle size and area are invariant. i.e.
|
Length PQ = Length P´Q´ |
|
|
Area |
PQR = Any point on the mirror line is invariant.
i.e. S
Reflection is an indirect transformation.
i.e. PQR is anti-clockwise.
P´Q´R´ is clockwise.
A line and its image will meet on the mirror line (unless the line is parallel to the mirror line).
i.e. Line PR and line P´R´ meet at V.
Reflection is an isometry.
i.e.
See examples of reflections − 
Location of Mirror Line
|
To find the mirror line given a line and its image: 1. Join the point and its image with a line. 2. Draw the perpendicular bisector of this 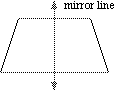line. |
 image of line |
Download an interactive spreadsheet (Microsoft Excel) showing reflections, rotations, translations and enlargements.
(Windows users, right click and "Save target as..." to save the files on your computer.)
