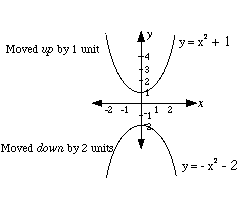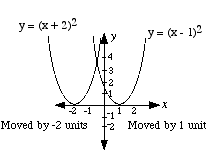Quadratic Functions

Parabola_Water.jpgQuadratic functions have graphs that are parabolas.
The general equation of a quadratic function can be given in two forms:

y = ax 2 + bx + c    OR        y = a(x − h) 2 + k

In both forms the highest exponent of x is 2.

The vertex, stationary point or turning point gives either the maximum or minimum value of the function.

Sketching Parabolas

Method 1: Factorisation.

If the equation is in the form y = ax2 + bx + c the following method should be used:

Step (a)  Factorise the function.
Step (b)  Find the x- and y-intercepts by putting y = 0 and x = 0.
Step (c) 
 
 
Find the axis of symmetry − always midway between the two x-intercepts.
Step (d)
 
Find the coordinates of the vertex or turning point. Example

 

 

 

 

Method 2: Transformation.

This method finds the coordinates of the vertex.
The y-intercept is found by putting x = 0.

The graph of the basic parabola y = x2 is shown in the diagram.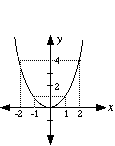Y11_Quadratic_Functions_01.gif

 

This basic parabola is moved or transformed as follows:

 

(a) y = ax 2 The a has the effect of changing the

parabola in the y- direction.

It affects the steepness of the graph.

  • If a is large, the parabola is steeper.
  • If a is negative, the parabola is inverted.
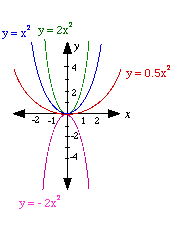Y11_Quadratic_Functions_02.gif

(b) y = x 2 + k

The k has the effect of moving the parabola along the y-axis by k units.

 

Y11_Quadratic_Functions_03.gif

(c) y = (x − h)2

The h has the effect of moving the basic parabola along the x-axis by h units.

 

Y11_Quadratic_Functions_04.gif


Download an interactive spreadsheet (Microsoft Excel) showing the transformation of parabolas.

button_download.gif

(Windows users, right click and "Save target as..." to save the files on your computer.)

Note
If the function does not factorise, either complete the square (example), or use the quadratic formula.

If the function has no roots, i.e. It does not factorise and the quadratic formula cannot be used (the discriminant is negative) then some points have to be plotted.