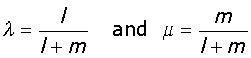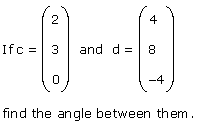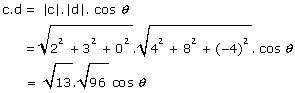Scalar Product and the Ratio Theorem

Scalar Product

Vectors can be added and subtracted and also multiplied by a constant. Vectors can also be multiplied.

The scalar product, or dot product, of two vectors a and b, in two or three dimensions, is defined as the product of their lengths and the cosine of the angle between their directions. It is written a.b and in words is said as "a dot b".

a.b = |a||b| cos θ

The angle θ can be acute or obtuse.

Properties of Scalar Products

  • Scalar products are commutative. That is a.b = b.a
  • a.a = |a|2 
    This is because the angle between vector a and vector a is 0o and cos 0o is equal to 1.
  • If neither a nor b is the zero vector then a and b are perpendicular if a.b = 0
    This is because the angle between perpendicular vectors is 90o and cos 90o is equal to 0.
  • If the value of a.b is known then the angle between the two eactors can be found as:

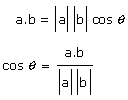
    Y11_Scalar_Product_and_the_Ratio_Theorem_01.gif
Scalar Product in Component Form

It can also be shown that if

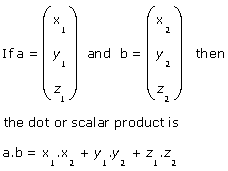
Y11_Scalar_Product_and_the_Ratio_Theorem_02.gif

Examples

Question
Answer
If Y11_Scalar_Product_and_the_Ratio_Theorem_03.gif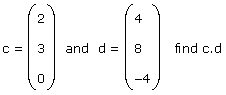

c.d = 2 x 4 + 3 x 8 + 0 x -4

= 8 + 24 + 0

= 32

Y11_Scalar_Product_and_the_Ratio_Theorem_04.gif

The scalar product of c and d is found in two different ways.

c.d = 2 x 4 + 3 x 8 + 0 x -4
= 8 + 24 + 0
= 32

Y11_Scalar_Product_and_the_Ratio_Theorem_05.gif

Therefore,

32 = √13.√96.cosθ
cosθ = 32/ √13.√96
cosθ = 0.9058
θ = 25.1 o

The angle between c and d is 25.1o

The Ratio Theorem

This theorem is very useful for finding the coordinates of a point that divides a line into a certain ratio.

 

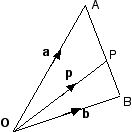
If P is any point on a line AB, and if, a, b and p are the position vectors of A, B and P respectively, then

Y11_Scalar_Product_and_the_Ratio_Theorem_06.jpg

p = λa + μb

and the ratio AP : PB =μ: λ for the constants λ and μ such that μ + λ =1

μ = AP/(AP + PB)

and

λ =PB/(AP + PB)_

Example

Question
Answer

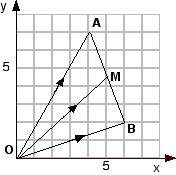
Point A has coordinates (4, 7) and point B has coordinates (6, 2).

Mark M, the midpoint of AB. What is the position vector, OM.

a. Y11_Scalar_Product_and_the_Ratio_Theorem_07.jpg

Using p = λa + μb where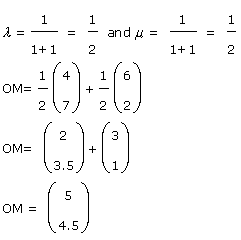

Y11_Scalar_Product_and_the_Ratio_Theorem_08.gif
 

Division of a Line

The table below shows examples of internally and externally dividing a line.

Internal Division
External Division

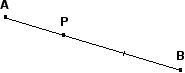
Point P dividing AB internally in the ratio 1:2

Y11_Scalar_Product_and_the_Ratio_Theorem_09.jpg

In problems, to find the ratios for λ and μ:

μ = 1/(1+2) = 1/3

λ = 2/(1+2) = 2/3

Note that λ + μ = 1

 

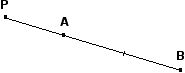
Point P dividing AB externally in the ratio 1:3.

(This can also be said as 1:-3, the negative sign indicates the division is external)

Y11_Scalar_Product_and_the_Ratio_Theorem_10.jpg

In problems, to find the ratios for λ and μ:

μ = -1/(1+1) = -1/2

λ = 3/(1+1) = 3/2

Note that λ + μ = 1

In general , if P divides AB in the ratio m : l then

Y11_Scalar_Product_and_the_Ratio_Theorem_11.gif