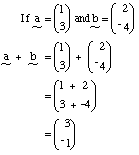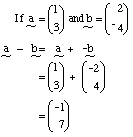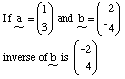BestMaths Online

Vectors

Vectors were covered in Year 10, Topic 16. To summarise this topic:

Representation of Vectors
Vectors are labelled either or  , sometimes . In textbooks they are often shown in bold type. e.g. AB or a. Each type of notation is used in this section.
Vectors can also be represented by a 2 X 1 column matrix . e.g. 
Vectors can be shown by a line giving its length and direction. e.g.shows the vector . 
In some texts the arrow is drawn at the end of the vector.

Multiplication of a Vector by a Scalar
A vector can be multiplied by a scalar or constant. Each component of the vector is multiplied by the scalar.

e.g. . The vector kb is the vector b multiplied by the scale factork.
It is in the same direction as b and k times the magnitude (length).

Inverse of a Vector
The inverse of a vector is obtained by changing the signs of the components of the vector.
e.g. 
This has the effect of changing the direction of the arrow on the vector.

Length of a Vector

The length of a vector (called its magnitude) can be found using Pythagoras' Theorem.
For the vector = , its magnitude is = √(x² + y²)

Addition and Subtraction of Vectors
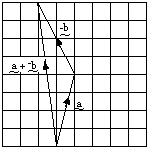
Vectors may be added using vector triangles.The second vector is added on to the end of the first vector. Note that the arrows on the two vectors being added go in one direction around the triangle and the arrow of the resultant vector goes the opposite direction.

When subtracting, using a diagram, add the opposite or inverse matrix. a − b is drawn as a + (-b). 

Addition
Vectors can be added together.

By matrices. Add the corresponding elements.

e.g. 

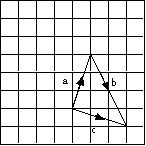
By drawing. Form a triangle. The second vector is added on to the end of the first vector. The resultant vector (labelled c) is sometimes shown by two arrows. Note that the two vectors go clockwise around the triangle and the resultant goes anti-clockwise.

e.g. is shown in the diagram.

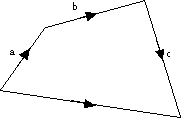
More than two vectors can be added together.

e.g.

---

Subtraction
Vector subtraction is best done by addition of the inverse or opposite vector.

By matrices 

By drawing

e.g

Practice vector calculations and diagrams − Vector Practice

Vector Algebra

Vector addition is commutative: p + q = q + p

and also associative: (p + q) + r = p + (q + r).

The zero vector, 0, is the vector that results in no translation or movement. In terms of vectors:

p + (-p) = 0
0p = 0
p + 0 = p

In this topic we will further develop ideas involving vectors, these will include base unit vectors, position vectors, the ratio theorem, vectors in three dimensions and the scalar product.

Base Unit Vectors
The vectors  and  are called basic unit vectors in the x and y directions respectively. 
They are denoted by the letters i and j. 
The vector p =  can be written in the form p = xi + yj

The following table illustrates how vectors can be written in terms of unit vectors:

matrix form	unit vectors
	3i + 2j
	-2i + j
	- 2.5j

This means that we can now do vector addition in two ways.

matrix form	unit vectors
+ =	(3i + 2j) + (-2i + j) = i + 3j
2 − 3 =	2(3i + 2j) − 3(-2i + j) = 6i + 4j + 6i − 3j = 12i + j

Position Vectors

Vectors such as  = represent a translation starting at A and moving to B. This type of vector is called a displacement vector.

A position vector is a special type of vector that starts at the origin O and ends at another point.

e.g. The position vector starts are the point O, (0,0) and finishes at the point P.

The position vector of the point P, with coordinates (a, b) is

An important property of displacement and position vectors gives equation  = b - a

where is the displacement vector from A to B and a and b are the position vectors of point A and point B.

From the diagram: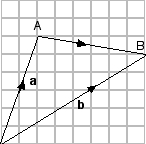 

a +  = b
 = b − a

Remember this important result:

= b − a

 

---