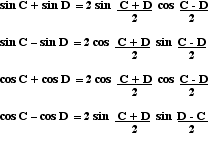Angle Formulae

There are four sets of formulae which make the solving and manipulation of trigonometric equations and identities easier.

These are:

All of these formulae are all provided in the tables issued for most examinations, although, as always, it is useful if you can memorise them.

You are not required to learn how they are derived but you should be able to follow the working.

The formulae and proofs are listed below, along with examples of their use.

Compound Angle Formulae

Trigonometric expressions such as sin (45 + 60) do not expand in a similar way to algebraic expansions.

i.e. sin (45 + 60) ≠ sin 45 + sin 60, instead the following formulae apply.

(Two proofs are given, the other formulae can be proven in a similar manner.)

sin(A + B) = sin A cos B + cos A sin B

sin(A − B) = sin A cos B − cos A sin B

cos(A + B)= cos A cos B − sin A sin B             

cos(A − B) = cos A cos B + sin A sin B   proof

Y12_Angle_Formulae_01.gif   proof

 Y12_Angle_Formulae_02.gif            

Note the "reversal" of signs in the cosine formulae.

Example

Simplify cos (180 − A)

cos (180 − A) = cos 180.cos A + sin 180. sin A = -1.cos A + 0.sin A = -cos A

Double Angle Formulae

A useful simplification of the compound angle formulae is when A and B are equal,
i.e. A + B = A + A = 2A

Again, trig functions do not obey algebraic rules, sin 2A ≠ 2sin A

By substituting into the compound angle formulae:

sin 2A = 2sin A cos A

cos 2A = cos2A − sin2A

cos 2A = 2cos 2A -1

cos 2A = 1 − sin2A

Y12_Angle_Formulae_03.gif

The three versions of the cosine double angle formulae are obtained using the
identity sin2 x + cos2 x = 1

Example

If sin x = 0.6 and cos x = 0.8, find the value of sin 2x

sin 2x = 2sin x cos x = 2 x 0.6 x 0.8 = 0.96

Product To Sum Formulae

These formulae are useful when the product of two trig functions need to be changed to a sum.

 

2sin A cos B = sin (A + B) + sin (A − B)    proof

2cos A sin B = sin (A + B) − sin (A − B)     proof

2cos A cos B = cos (A + B) + cos (A − B)    proof

2sin A sin B = cos (A − B) − cos (A + B)      proof

Example

Express the product 2sin 40° cos 30° as a sum of two trig. functions.

2 sin 40° cos 30° = sin (40 + 30)° + sin (40 − 30)° = sin 70° + sin 10°

 

Sum to Product Formulae

The sum of two trig functions is not obtained by adding the two angles together.

e.g. sin 40° + sin 30° ≠ sin 70°

These formulae are needed when the sum of two trig functions is changed to a product.

 

 

Y12_Angle_Formulae_04.gif

Example

Express the sum sin 40° + sin 30° as the product of two trig. functions.

sin 40° + sin 30° = 2 sin (40 + 30)°/ 2 cos (40 − 30)°/ 2 = 2 sin 35° cos 5°