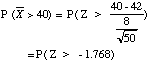The theory for the Central Limit Theorem was developed in the previous topic Distribution of the Sample Mean.
The central limit theorem states:
| If random samples of size n are taken from ANY distribution with mean μ and variance σ 2then, for large n, (say, over 30), the distribution of the sample mean is approximately normal, with mean μ and standard deviation |
When solving probability problems using the Central Limit Theorem, the z-score formula becomes ![]()
Example
|
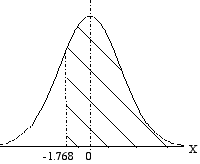
A sample of size 50 is taken from a normally distributed population with a mean of 42 and a standard deviation of 8. Find the probability that the sample mean is greater than 40. |
|
|
Distribution of sample means is normal with mean μ = 42 and σ = 8 / √50 Using Central Limit Theorem:
= 0.5 + 0.4615 = 0.9615 |
 |