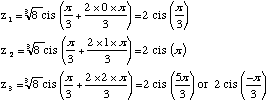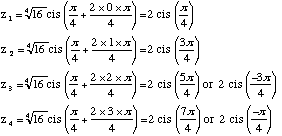BestMaths Online

Consider the rule for multiplying complex numbers in polar form

z ₁z ₂ = r ₁ cis θ₁ . r ₂ cis θ ₂

          = r ₁r ₂ cis (θ ₁ + θ ₂)

Squaring Complex Numbers

Suppose that the two numbers are equal. i.e. z ₁ = z ₂

Then z² = r cis θ. r cis θ = r²cis(θ + θ)

(r cis θ) ² = r² cis(2θ)

Cubing Complex Numbers

Let z₁ = r cis θ and z₂ = r cis(2θ)

Then z³ = r cisθ. r cis(2θ) = r cis(θ + 2θ)

(r cis θ) ³ = r³ cis(3θ)

De Moivre's Theorem

The above two derivations can be extended into a general rule known as De Moivre's Theorem:

Example

Find (3 cis )⁶

(3 cis )⁶ = 3⁶ cis 6. = 729 cis 

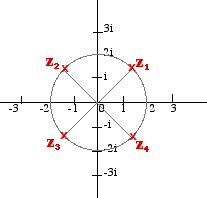
Equations involving Complex Numbers

The aim of this section is to solve equation of the type zⁿ = r cis θ

Taking the nth root of both sides z = (r cis θ)^1/n

By De Moivre's Theorem

This provides one of the roots but because complex numbers in polar form repeat every 360° or 2π radians there will be other roots as well.

The full solution set of the nth roots of r cis θ is given by:

This will mean that when finding the nth root there will be n solutions.

Example 1

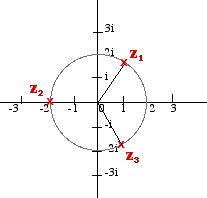
Note that the three roots are equally spaced around a circle of radius 2 (cube root of 8) on the Argand diagram. This is true for all equations of the form zⁿ = r cis θ. Once one root has been found the other roots can be placed, equally spaced, around a circle of radius the n th root of r.

Example 2