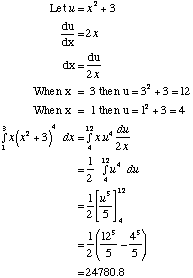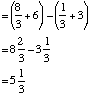One of the uses of integration is to find the area between a curve and the x-axis.
These areas are found be evaluating a definite integral. When anti-differentiating the result is a function. When evaluating a definite integral the answer is a number.
Defiinite Integrals
A definite integral is calculated by integrating a function between two values, called the limits of integration. These two values are substituted into the integrated function and the difference taken.
The formula is:
|
where F(x) is an anti-derivative of f(x) |
This complicated looking formula is easier to use than it looks. It simply means doing the following:
| Method |
Example Evaluate |
|
| Step 1 | Integrate the function | = |
| Step 2 | Substitute the values 2 and 1 |
= |
| Step 3 | Evaluate |
|
| Note that the constant of integration c is not shown as it would be eliminated when subtracting. | ||
Definite Integration by Substitution
If the method of integration used is substitution, the limits of integration are changed to those of the variable used in the substitution.
Example
![]()