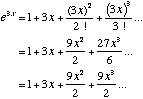In Year 12, the exponential function f(x) = ex was studied. It is the only function which is its own derivative.
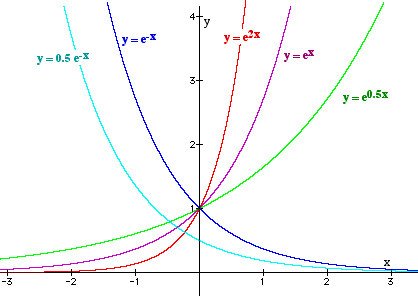
This means that at any point on the graph of the exponential function y = ex the gradient of the curve at that point is equal to the value of the function (the y-value) at that point.
Graphs of Exponential Functions
The Exponential Series
The function y = e x can also be written as a series :
It can be seen that if this series is differentiated term be term the result is the same series!
(This formula is provided in the tables given with the Bursary examination. Try to memorise it and learn how to use it.)
Example
Write e3x as an exponential series for the first four terms.
This means that the polynomial expression above, called a power series is a close approximation for ex.
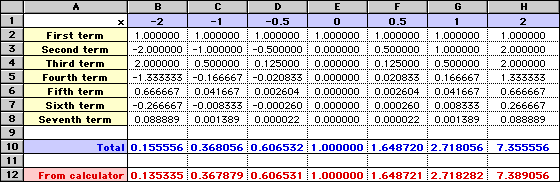
To see how close the approximation becomes a spreadsheet is used below to evaluate e for values of x from -2 to +2 for the first seven terms of the series (to 6 decimal places).
The sum of these seven terms is then compared with the calculator value of ex for the same values.
It can be seen how close these values are especially for -1 ≤ x ≤ 1. The closeness would increase if even more terms were taken.
The spreadsheet formulae used to give these values were:
These may vary slightly depending on the spreadsheet used. These were created in Appleworks.
The exponential series always converges as the denominator of each term gets larger so each term gets smaller.
The General Term of the Exponential Series
The general term of the exponential series is given by:
 |
Note that for the 6th term r = 5
Example Find the 7th term for the exponential series e2x
t 7 = t 6+1 =
