In this topic, more difficult quadratic equations, equations involving fractions and algebraic fractions, equations requiring completing the square and equations involving logarithms and indices will be covered.
More Difficult Quadratic Equations
There are several ways to solve quadratic equations, these include:
|
Method and
Example |
Solution
|
||||||||||||||||||||||||
|
Taking the square root Solve (x − 3)2 = 64 |
x + 3 = ± 8 (taking square root of both sides) |
||||||||||||||||||||||||
|
Factorisation 2√x = 60 − 2x |
The answer of 36 when substituted back into the equation does not balance and is not a valid solution. This shows the importance of checking all solutions if you have squared an equation. |
||||||||||||||||||||||||
|
Completing the square x2 + 4x − 1 = 0 |
|
||||||||||||||||||||||||
|
Quadratic formula 2x2 = 5x − 1 |
2x2 = 5x − 1
|
Equations with Fractions or Algebraic Fractions
The best way, which works in all cases, is to multiply each term in the equation by the common denominator.
|
Example 1
|
Example 2
|
Solve  |
Solve  |
 |
 |
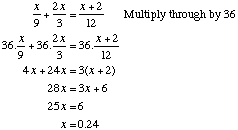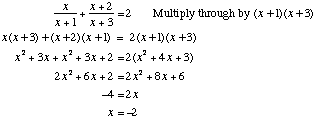Equations with Logarithms and Indices
Solving these types of equations rely on the properties of logarithms and indices.
Simple index equations such as 4x = 64 can be solved using the properties of exponents.
4x = 64
4x = 43
Therefore x = 3
Logarithms can be used to solve more complex equations involving indices, which are not able to be solved using other methods.
|
Example 1
|
Example 2
|
| Solve 20 = 10e5x | Solve 3x = 7 |
|
20 = 10e5x 2 = e5x (dividing both sides by 10) ln 2 = ln e5x (taking logs to base e of both sides) ln 2 = 5x (definition of logarithms) x = 0.14 (to 2 s.f.) |
3x = 7 Take logs to base e of both sides ln 3x = ln 7 x ln 3 = ln 7 (using properties of logs) x = ln 7 / ln 3 x = 1.77 ( to 3 s. f.) |
Further Examples
e.g. 3x = 10. (There is no conventional way to solve this equation.)
The method used is to "take logs" of both sides of the equation.
