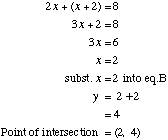Linear programming involves modelling a real life situation using a series of inequalities as constraints and then finding an optimal solution for the situation. Most of the problems involve the same procedures and require skill with sketching inequalities and solving pairs of simultaneous equations.
Sketching Linear Inequalities
|
Action
|
Method
|
Notes
|
|
| Step 1 | Sketch the straight line | Put x = 0 to find the y-intercept |
A solid line if the inequality contains ≥ or ≤ A dotted line if the inequality contains > or < |
| Put y = 0 to find the x-intercept | |||
| Step 2 | Shade the correct side of the line | Test with the point (0, 0) | If more than one inequality,SHADE OUT the region required. |
Example
|
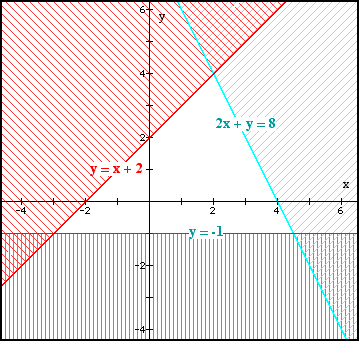
On the same set of axes sketch the following inequalities (use shading out). 2x + y ≤ 8 y ≥ -1 y ≤ x + 2
The intercepts are:
Shading correct regions:
Note: The areas obeying each inequality have been shaded OUT. The required region is the white triangle.
|
 |
Intersection of Lines
The points of intersection of the lines can either be read off the graph, if they are obvious, or found by solving the equations of the two lines concerned simultaneously.
For the diagram above we will solve each pair simultaneously:
|
Top point
|
Left point of intersection
|
Right point of intersection
|
|
2x + y = 8 ........A |
y = x + 2 ........A y = -1............. .B |
2x + y = 8 .........A |
|
Substitute B into A
|
Substitute y = -1 into A -1 = x + 2 x = -1 -2 x = -3 Point of intersection = (-3, -1) |
Substitute y = -1 into A 2x + -1 = 8 2x = 9 x = 4.5 Point of intersection = (4.5, -1) |
All of the above skills are needed to solve word problems on linear programming and optimisation.
Linear Programming
The steps for solving linear programming problems are as follows:
- Step 1 Write down the inequalities (constraints) from the problem.
- Step 2 Write down the function to be optimised. (Often maximum profit or output).
- Step 3 Sketch and shade the region which satisfies all of the inequalities.
- Step 4 Find the coordinates of the vertices of the region (the nearest whole number coordinates may be required).
- Step 5 Substitute these coordinates into the function to be optimised to find the maximum or minimum value.
Example
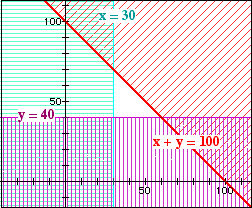
A fruit shop makes $8 profit on every tray of kiwifruit it sells and $6 profit on every tray of strawberries it sells.
It always sells 30 or more trays of kiwifruit and 40 or more trays of strawberries each week. It has never sold more than 100 trays of the two fruit in total in any week. How many trays of each would the shop have to sell to make the maximum profit in a week.
Method
|
Step 1
|
Let the number of trays of kiwifruit sold be x. x ≥ 30 |
|||||||||
|
Step 2
|
Profit P = 8x + 6y | |||||||||
|
Step 3
|
Sketch the graph (shading out)
|
|||||||||
|
Step 4
|
The vertices of the white triangle are at (30, 40), (30, 70) and (60, 40) | |||||||||
|
Step 5
|
Substitute the coordinates of each point into profit equation:
|
|||||||||
|
Therefore, the maximum profit of $720 is when 60 trays of kiwifruit and 40 trays of strawberries are sold.
|
||||||||||
