When the value of n in a binomial distribution is large and the value of p is very small, the binomial distribution can be approximated by a Poisson distribution. If n > 20 and np < 5 OR nq < 5 then the Poisson is a good approximation.
The Binomial distribution tables given with most examinations only have n values up to 10 and values of p from 0 to 0.5
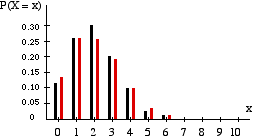
The similarities between the two distributions can be seen in the vertical line graph below.
 |
|
The black graph is a binomial distibution with n = 10 and p = 0.2 The red graph is a Poisson distribution with λ = 2 |
The value of the mean needed for the Poisson approximation is λ = np
To summarise:
|
For large values of n and small values of p, the Poisson distribution approximates the binomial distribution
|
|
| Test |
n > 20, np < 5 OR nq < 5 |
| New parameters |
λ = np |
Example
A factory puts biscuits into boxes of 100. The probability that a biscuit is broken is 0.03. Find the probability that a box contains 2 broken biscuits
Solution
This is a binomial distribution with n = 100 and p = 0.03.
These values are outside the range of the tables and involve lengthy calculations.
Using the Poisson approximation (test: np = 100 x 0.3 = 3, which is less than 5)
Let X be the random variable of the number of broken biscuits
The mean λ = np = 100 × 0.3 = 3
P(X = 2) = 0.224 (from tables)
The probability that a box contains two broken biscuits is 0.224.