The gradient of a function is a measure of the rate of change of the y-value compared to the x-value.
Increasing Functions
If the gradient is positive over a range of values then the function is said to be increasing. i.e the value of the y is increasing as x increases. On a graph the curve will be sloping up from left to right. e.g. 
For an increasing function f '(x) > 0
Decreasing Functions
If the gradient is negative over a range of values then the function is said to be decreasing. i.e the value of the y is decreasing as x increases. On a graph the curve will be sloping down from left to right. e.g.
For a decreasing function f '(x) < 0
Stationary Points
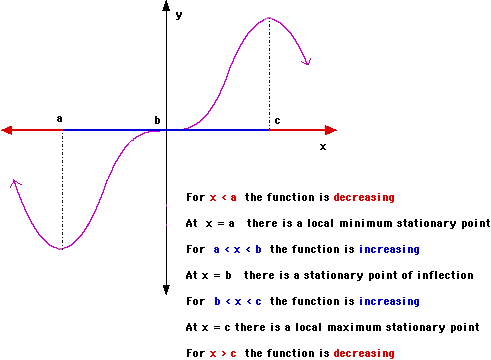
If the gradient of a curve at a point is zero, then this point is called a stationary point. This can be a maximum stationary point or a minimum stationary point. They are also called turningpoints. For a stationary point f '(x) = 0
Stationary points are often called local because there are often greater or smaller values at other places in the function.
Another type of stationary point is called a point of inflection. With this type of point the gradient is zero but the gradient on either side of the point remains either positive or negative.
The diagram below shows examples of each of these types of points and parts of functions.
Concavity
Every curve contains something called concavity, which may be either
|
Concave down
|
Concave up
|
Both types of concavity
|
 |
 |
 |
A point of inflection is one where the curve changes concavity. A point of inflection does not have to be a stationary point, although as we have seen before it can be.
Finding Stationary Points and Points of Inflection
First derivative test
Differentiating once and putting f '(x) = 0 will find all of the stationary points. Examining the gradient on either side of the stationary point will determine its nature, i.e. Maximum, minimum or point of inflection.
Example
| Method |
Example Find the coordinates and nature of the stationary point(s) of the function f(x) = x3 − 6x2 |
||||||||||||||||||||||||||||||||
|
Step 1
|
Differentiate the function to find f '(x) | f '(x) = 3x2 − 12x | |||||||||||||||||||||||||||||||
|
Step 2
|
Put f '(x) = 0 as the gradient at the stationary points is zero. | 3x2 − 12x = 0 | |||||||||||||||||||||||||||||||
|
Step 3
|
Solve this equation to find the x-value of the stationary point. | 3x(x − 4) = 0 x = 0 or x = 4 |
|||||||||||||||||||||||||||||||
|
Step 4
|
Substitute this value into the original function to find the y-value of the stationary point. |
When x = 0, y = 0 − 0 = 0 When x = 4, y = 64 − 96 = -32 Coordinates of the turning points are |
|||||||||||||||||||||||||||||||
|
Step 5
|
Examine the gradient on either side of the stationary point to find its nature.
|
Choose values either side of the turning points
This shows a maximum point followed by aminimum point.
|
Second derivative test
Differentiating once determines the gradient of a curve and putting f '(x) = 0 will find all of the stationary points.
Differentiating a second time to find f ''(x) and evaluating it for a particular point will determine the nature of the point.
|
f '(x)
|
f '' (x)
|
Nature of point
|
|
0
|
positive
|
A local minimum point
|
|
0
|
negative
|
A local maximum point
|
|
positive
|
0
|
increasing point of inflection
|
|
negative
|
0
|
decreasing point of inflection
|
|
0
|
0
|
Rare, but could be any of the above! |
Note The second derivative determines concavity:
|
y '' < 0
|
Concave down |
|
y '' > 0
|
Concave up |
Example
Use the first and second derivative tests to find the coordinates and nature of the turning points of the function f(x) = x3 − 3x2 − 45x
First derivative f '(x) = 3x2 − 6x − 45
Let f '(x) = 0
3x2 − 6x − 45 = 0
3(x − 5)(x + 3) = 0
x = -3 or x = 5
Second derivative f ''(x) = 6x − 6
When x = -3, f ''(-3) = -24 and this means a MAXIMUM point.
When x = 5, f ''(x) = 24 and this means a MINIMUM pont.
Finally, evaluate y at each point.
f(-3) = 81 and f(5) = -175
So the two turning points are a local maximum at (- 3, 81) and a local minimum at (5, -175)
Note The alternative notation of y ' for the first derivative and y '' for the second derivate can also be used.
