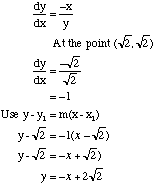Tangents and Normals

By differentiating and finding the derived or gradient function we obtain an equation which will give the gradient at any point on the curve. The gradient for a particular value of x can then be obtained by substitution.

 

Finding the Equation of the Tangent to a Curve

Once the gradient of a tangent to a curve has been found, the formula y − y1 = m(x − x1) can be used to find the equation of the tangent at the point (x1, y1).

Example
Find the equation of the tangent to the circle x2 + y2 = 4 at the point (√2, √2)

There are two methods for solving this problem.

Method 1 Use implicit differentiation Method 2 Use parametric equations

Differentiating implicitly:

2x + 2y. Y12_Tangents_and_Normals_01.gif = 0

Y12_Tangents_and_Normals_02.gif

The parametric equations for x2 + y2 = 4 are:

x = 2cos t and y = 2sin t

Y12_Tangents_and_Normals_03.gif = 2cos t ÷ -2sin t = -cot t

When x = √2

2cos t = √2

cos t = √2/ 2

⇒ t = π/ 4 (or − π/ 4)

Thus the gradient at point (√2, √2) is:

cot (π/ 4) = -1

Hence the equation is:

y − √2 = -1(x − √2)

y = -x +2√ 2

 

Finding the Equation of the Normal to a Curve

The normal to a tangent to a curve at a point is the line perpendicular to the tangent at the point of contact.

If a line with gradient m1 is perpendicular to another line with gradient m2 then m1 x m2 = -1. ⇒ m1 = -1/ m2

Example

Find the equation of the normal to the curve x2 + y2 = 4 at the point (√2, √2)

The two methods shown above can be used to find that the gradient of the tangent at (√2, √2) is m = -1

The gradient of the normal is m = -1/ -1 = 1

Hence the equation is:

y − √2 = 1(x − √2)

y = x