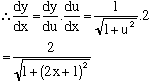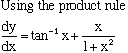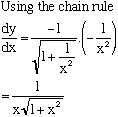Each of the basic trigonometric functions can be differentiated.
Derivatives of sin x, cos x and tan x
|
If f(x) = sin x then f '(x) = cos x |
|
If f(x) = cos x then f '(x) = − sin x |
|
If f(x) = tan x then f '(x) = sec2x |
Examples using Chain Rule
|
Differentiate f(x) = sin 4x f '(x) = 4 cos 4x |
Differentiate f(x) = 4 cos 2x f '(x) = 2. 4. -sin 2x = -8 sin 2x |
Derivatives of sec x, cosec x and cot x
|
If f(x) = sec x then f '(x) = sec x tan x |
|
If f(x) = cosec x then f '(x) = − cosec x cot x |
|
If f(x) = cot x then f '(x) = − cosec2x |
Examples using Chain Rule
|
Differentiate f(x) = cot (3x + 2) f '(x) = 3. -cosec2 (3x + 2) = -3cosec2 (3x + 2) |
Differentiate f(x) = sec 4x f '(x) = 4 sec 4x tan 4x |
Derivatives of the Inverse Trigonometric Functions
For more complex inverse trig. functions the following can be used.
These formulae are often provided for tests and examinations. Make sure you check with your teacher whether they are provided.
Examples
1. Differentiate y = sin-1(2x + 1)
Let u = 2x + 1 ∴ y = sin-1u
2. Differentiate y = x tan-1x
3. Differentiate y = sec-1x = cos-1 1/x
