The earlier introduction to Trigonometry should be understood before moving into the Year 12 Trigonometry topics.
This first topic revises previous work on trigonometrical graphs, with slightly harder exercises.
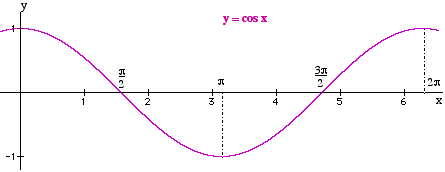
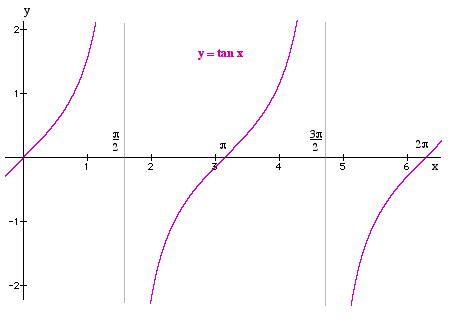
The graphs of the functions of the three basic trigonometic ratios, y = sin x, y = cos x and y = tan x are shown below.
The x-axis units are radians. Remember: 180° = π radians.
These graphs are called periodic functions because the pattern repeats itself over and over.
The frequency with which it does this is called the period of the function.
The amplitude of the graph is the distance between the x-axis and the highest point on the graph.
The frequency of the graph is the number of times the graph repeats itself over 2π or 360°
y = sin xThe period of the graph is 2π or 360°. The amplitude of the graph is 1. There are no asymptotes. The domain is ℜ the set of real numbers. The range is The frequency is 1 |
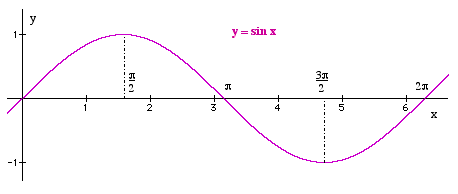 Click Here to see the graph of y = sinx being formed. |
y = cos xThe period of the graph is 2π or 360°. The amplitude of the graph is 1. There are no asymptotes. The domain is ℜ the set of real numbers. The range is -1≤ y ≤ 1 The frequency is 1 |
 Click Here to see the graph of y = cosx being formed. |
y =tan xThe period of the graph is π radians or 180°. There are asymptotes every π radians or 180°. The domain is ℜ the set of real numbers except where the asymptotes occur. The range is the real numbers ℜ The frequency is 2 |
 Click Here to see the graph of y = tanx being formed. |
Transformations of the Basic Trigonometric Functions
More complicated trigonometric functions of the form y = AsinB(x − C) +D and y = AcosB(x − C) + D can be sketched by transforming the basic graphs shown above. The constant D, not mentioned in the Bursary prescription, is also considered. Each of the variables A, B, C and D change either the shape or position of the basic graphs.
|
Type of function
|
Feature changed
|
Transformation required
|
Examples
|
|
y = A sinx y = A cos x |
the amplitude
|
The basic graph is compressed or stretched along y-axis by scale factor A. The new ampitude is A |
|
|
y = sin Bx y = cos Bx |
the period
|
The basic graph is compressed or stretched along x-axis by scale factor B. The new period is 360° ÷ B |
|
|
y = sin(x − C) y = cos(x − C) |
the position
|
The basic graph is translated along the x-axis by C. For (x − 30°) the graph moves 30°to the right. |
|
|
y = sinx + D y = cos x + D |
the position
|
The basic graph is translated along the y-axis by D. If D is positive the graph moves UP |
Putting it all together...
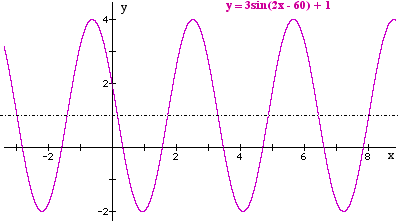
| Sketch the graph of y = 3sin2(x - 30) + 1 |
3 |
Changes amplitude to 3 |
|
2
|
Changes period to 360 ÷ 2 = 180° | |
|
x - 30
|
Moves graph right by 30° | |
|
+1
|
Moves graph up 1 |
The graph looks like this:
It is unlikely that you will be asked to perform all four of these transformations for one graph!
