|
Many calculations involve money.

Coins and Notes
In New Zealand, the coins and notes available are as follows:
|
Coins
|
5 cents
|
10 cents
|
20 cents
|
50 cents
|
$1
|
$2
|
 |
|
Notes
|
$5
|
$10
|
$20
|
$50
|
$100
|
|
Because the smallest coin is worth 5 cents, amounts of money often have to be rounded to the nearest 5 cents.
 |
81 cents and 82 cents would be rounded down to 80 cents
83 cents and 84 cents would be rounded up to 85 cents
86 cents and 87 cents would be rounded down to 85 cents
88 cents and 89 cents would be rounded up to 90 cents |
This system is called Swiss Rounding and is used by most shops and supermarkets in New Zealand.
If several items are being purchased the rounding is done on the total cost of the items.
Money Calculations
Numbers of dollars and cents can be written as dollars using decimals:
Five dollars and 35 cents is written $5.35
Ten dollars and five cents is written $10.05
The rules that apply to decimals also apply to money calculations:
|
Example
|
Answer
|
 |
| Calculate $45.32 + $9.95 |
|
| Calculate $40 − $21.95 |
|
| Calcualte $25.50 x 8 |
|
| Calculate $27 ÷ 6 |
|
Calculations involving Percentages and Money
 |
Example
|
Answer
|
| Find 25% of $500 |
25% of $500 = 500 × 0.25 = $125
|
|
I earn $620 interest on an investment of $25,000.
What percentage is this?
|
Percentage interest = 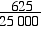 × 100 = 2.5% × 100 = 2.5%
|
For more difficult calculations involving money and percentages, go to Topic 49.
Money Applications
|
Applications
|
| a |
I go to the supermarket and buy 6 bars of chocolate at $1.30 each, a bag of carrots at $2.40 and 2 dozen eggs at $2.50 per dozen.
How much do I spend?
|
Total spent
= 6 × 1.30 + 2.40 + 2 × 2.50
= 7.80 + 2.40 + 5.00
= $15.20
|
| b |
At the cinema I pay for myself and my four friends.
The total cost is $47.50. How much is the cost per person?
How much change would I get from a $50 note?
What percentage of $50 have we spent?
|
Cost per person = $47.50 ÷ 5 =$9.50
Change from $50 = 50 − 47.50 = $2.50
% spent = (47.5/ 50) × 100 = 95%
|
|
c
|
How much change would I get from $20 when I purchase the following:
(i) 6 packets of chips at $1.84 each?
(ii) 6 free-range eggs at $3.86 per dozen?
|
|
(i) Cost of chips = 6 × 1.84 = $11.04
Rounded to $11.05
Change from $20 = 20 − 11.05 = $8.95
(ii) Cost of eggs = 3.86 ÷ 2 = $1.93
Rounded to $1.95
Change from $20 = 20 − 1.95 = $18.05
|
|





