Probability

Normal_Distribution.jpgRelative frequency

Relative frequencies give an indication of how often an event might occur.
Relative frequencies can be shown as fractions, decimals or percentages.

Example
100 teenagers were asked what their favourite flavour out of five types of ice-cream was and the results were recorded in a frequency table.

The relative frequency is the FRACTION or PROPORTION of people in that particular category.

e.g. 20 out of the 100 teenagers liked strawberry ice-cream
so 
the relative frequency of strawberry ice-cream being chosen is 20/100 = 0.2 = 20%

Notice that the relative frequencies always add up to 1 or 100%.

Based on these results it is more likely that the next person asked would like chocolate ice-cream as it has the highest relative frequency.

How likely an event is to happen can be predicted by its relative frequency.

Relative frequency
Likelihood of event happening
Above 90%
Very likely to happen
Above 50%
Likely to happen
Below 50%
Unlikely to happen
Below 10%
Very unlikely to happen

Relative frequencies are usually the result of an experiment or survey.


Probability

Probabilities give an indication of the chance that an event will happen.
Probabilities can be expressed as fractions, decimal fractions or percentages.

The probability of an event happening = Probability_01.gif

Some examples:

Event 1
Probability

That a head will be face up, when a coin is tossed .

1/2 or 50% or 0.5
Event 2
Probability

That a 2 will be face up when a dice is thrown.

1/6 or 16.7% or 0.17
Event 3
Probability
That the first ball to come out in a Lotto draw is number 22. (There are 40 balls.) 1/40 or 2.5% or 0.025

 

The lowest probability is 0.

If the probability of an event happening is 0, the event cannot occur.

e.g. P( throwing a six-sided die and scoring a 7) = 0

The highest probability is 1.

If the probability of an event happening is 1, the event is certain to occur.

e.g P( throwing a six-sided die and scoring less than 7) = 1

Tree Diagrams

A tree diagram can help to solve probability problems or problems involving the number of ways that things can be carried out.

e.g. A car can be bought in two colours, blue and red. Each car can be bought with or without air conditioning. How many different combinations can be chosen?

A tree diagram helps solve this problem.

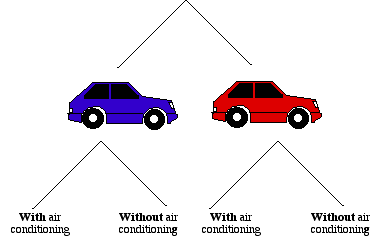
Probability_02.gif

There are four possible combinations available to the car buyer.

Probabilities and Tree Diagrams

If the probabilities of the events on a tree diagram are known, then the probability of each combination occuring can be calculated.

If there were 6 blue cars and 4 red cars, and the probability of any car having air conditioning was 0.5, then the following additions could be made to the diagram.

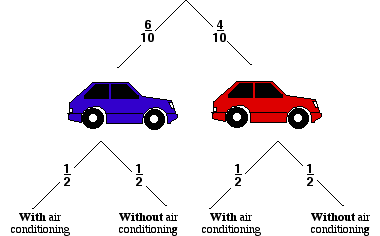
Probability_03.gif

Notice that the fractions on each pair of "branches" always add up to 1.

From this diagram the probability of each combination being chosen can be calculated.

Combination
Probability
blue with air conditioning
Probability_04.gif
blue without air conditioning
Probability_05.gif
red with air conditioning
Probability_07.gif
red without air conditioning
Probability_08.gif

Notice that because all of the combinations are covered the probabilities add up to 1.

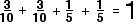(Probability_09.gif)