Problem Solving

There are many types of problems in mathematics. The answer or solution to a problem can often be obtained in several ways.

Solving problems in mathematics can be frustrating... but also very satisfying.

Y7_Problem_Solving_Baby_Mad.gif"How do you do this one?" Y7_Problem_Solving_Baby_Happy.gif"That was easy!"

Most problems can be solved by following a plan or strategy.

The following plan, which has four key steps, works well:

Step 1 Read the problem

What information is given in the question?
What are you being asked to find?
Step 2 Plan what to do

What method shall we use?
Is any extra information needed?
Would a diagram help?
Do we need to use a formula, or a calculator?
Step 3 Solve the problem Make the calculations required. 
Show each step of your working.
Write using full mathematical equations and statements
Step 4 Give the answer Does your answer make sense?
Does your answer need rounding?
Write the answer as a full sentence.

This plan can be summarised:

READ ---> PLAN ---> SOLVE ---> ANSWER

Other Hints on Problem Solving

Every problem is different but there are several approaches you can take which may result in progress being made:

  • Estimate the answer
  • Use trial and error (guess and check) until you get the correct answer.
  • Look for patterns
  • Use algebra and form equations
  • Make a table or list
  • Draw a diagram, graph or make a model
  • Break the problem up into parts.

Types of Problems

Example 1
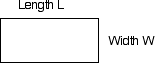
A rectangle is twice as long as it is wide. Its perimeter is 24 cm, What is its area?

Step 1 Read the problem

Key points: Shape is a rectangle, length = 2 x width, perimeter is 24 cm

To find: Area of rectangle
Step 2 Plan what to do

We need to remember that the perimeter is the distance around the shape and the area is the length multiplied by the width.
A diagram will help.
A table of possible lengths and widths might help.
Algebra might be useful
Step 3 Solve the problem

Y7_Problem_Solving1.gif

Make a table of possible widths and lengths:

Width (cm)

Length (cm)

 Perimeter (cm)
2
4
 2 + 2 + 4 + 4 = 12
3
6
 3 + 3 + 6 + 6 = 18
4
8
 4 + 4 + 8 + 8 = 24
5
10
 5 + 5 + 10 + 10 = 30


A width of 4 cm with a length of 8 cm gives the required perimeter.
Thus, the area is 4 × 8 = 32 cm2
Alternatively, you can use algebra:
L + L + W + W = 24
If the width = W, the length L = 2W
Form an equation: W + W + 2W + 2W = 24
6W = 24
W = 4

Therefore the width = 4 cm and the height = 8 cm
The area = 8 × 4 = 32 cm2
Step 4 Give the Answer The area of the rectangle would be 32 cm2.

Example 2

What are the next 3 numbers in the sequence 2, 5, 10, 17,...?

Step 1 Read the problem

The next three numbers are needed.
Step 2 Plan what to do

Look for a pattern
Use a table
Draw a graph
Step 3 Solve the problem

Method 1
Look for a pattern:

5 − 2 3
10 − 5 5
17 − 10 7
26 − 17 9
37 − 26 11
50 − 37 13

You would expect the gap between 17 and the next number to be 9, so the next number is 26. Following this pattern the next numbers are 37 and 50.

Method 2
Use a table:

1st number
2nd number
3rd number
4th number
5th number
6th number
7th number
12 + 1
22 + 1
32 + 1
42 + 1
52 + 1
62 + 1
72 + 1
2
5
10
17
26
37
50

Try to see a connection between the position of the number and the number itself.

The connection is that if you SQUARE the first number and ADD ONE you get the sequence number.

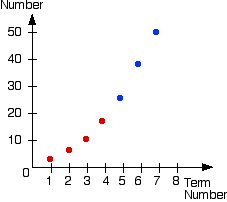
Method 3
Draw a graph:

Y7_Problem_Solving3.gif

The next three numbers (in blue) can be found from the graph . These sequence graphs are often straight lines.
Step 4 Give the answer The next three numbers are 26, 37 and 50.