BestMaths Online

Symmetry in Real Life 

If an object has symmetry or is symmetrical it has a balanced look. There is line symmetry which is similar to an object being seen in a mirror and rotational or turning symmetry which is about rotating objects around thier centre point. 

Buildings are often built to look symmetrical.	Designers love to design items with symmetry.	People are often quite symmetrical.	All of these drawings show line symmetry.

There are two types of symmetry: line symmetry, which involves reflection , and rotational symmetry, which involves rotation .

Line Symmetry

A figure has a line of symmetry if it maps or folds onto itself under reflection in the line. The figure is divided by the line into two parts which are identical.

e.g.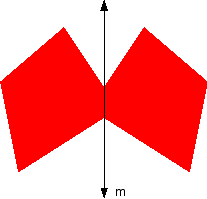 

Line m is called the mirror line or axis of symmetry.

Different shapes can have various numbers of axes of symmetry. e.g.

Name of shape	Diagram	Number of axes of symmetry
Square		4 (m, n, p and q)
Rectangle		2 (m and n)
Equilateral Triangle		3 (m, n and p)

Rotational Symmetry

A figure has rotational symmetry if it can be rotated around a point, called the centre of rotation so that if fits exactly onto itself.

All figures have an order of rotational symmetry of at least 1.

The order of rotational symmetry is the number of times the shape fits onto itself during a rotation of 360° 
(one complete turn).

e.g.

Name of shape	Diagram (the dot is the centre of rotation)	Order of rotational symmetry
Square		4 (90°, 180°, 270° and 360°)
Rectangle		2 (180° and 360°)
Equilateral triangle		3 (120°, 240° and 360°)

Total Order of Symmetry

The table shows the symmetry properties of some common shapes.

A figure has point symmetry if it maps onto itself under a rotation of 180° (a half turn). e.g. A parallelogram.