A circle is a shape formed by a curve such that all points on the curve are the same distance from a fixed point, called the centre.
Definitions
|
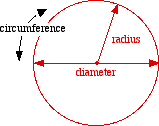
The circumference is the distance around a circle. A radius is the distance from the centre to any point on the circumference. A diameter is a chord that passes through the centre. An arc is a part of the circumference. A chord is a straight line joining two points on the circumference. A segment is an area of a circle bounded by a chord and the circumference. A sector is an area of a circle bounded by two radii and the circumference. A tangent is a line that touches the circumference of a circle at only one point. |
|
 |
π is a fixed number (called a constant). It is the ratio of the length of the circumference to the length of the diameter.
This ratio is the same for ALL circles.
π is an irrational number and cannot be calculated exactly but is equal to 3.141592 (to 7 significant figures)
A good fractional approximation to π is 22⁄7.
Circumference
 |
The perimeter of a circle is called the circumference C = 2π r = π d |
Area
|
Area of Circle A = π r2 |
Examples of Circle Calculations
|
Example 1
|
Circumference
|
Area
|
|
Find the circumference and area of a circle of radius 6 cm. Use π = 3.1 |
C = 2π r C = 2 × 3.1 × 6 C = 37.2 cm
|
A = π r2 A = 3.1 × 6 × 6 A = 111.6 cm2 |
|
Example 2
|
||
|
Find the area of the sector shown below if the radius of the circle is 8 cm.
Use π = 3.1 |
Angle of sector = 90° Fraction of circle = 90⁄360 = 1⁄4 Area of sector = 0.25 × Area of circle
|
|
|
Example 3
|
||
|
Find the radius of a circle that has a circumference of 55.8 cm. (Use π = 3.1) |
C = 2πr 55.8 = 2 × 3.1 × r
6.2r = 55.8 r = 55.8⁄6.2 r = 9 cm |
|
