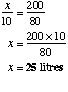A ratio compares two quantities of the same kind.
A ratio compares two quantities of the same kind.
Before simplifying a ratio, each quantity should be in the same units. e.g. $5 to $3 or 60 minutes to 30 minutes.
A ratio can be expressed in several forms. e.g. A ratio of 1 to 2 can be written 1 : 2 or 1⁄2 or 50%.
Ratios can be simplified like fractions. e.g. 50 : 25 can be reduced to 2 : 1.
|
1. Write the ratio 15 : 20 as: |
|
|
(a) A fraction |
(a)15⁄20 = 3⁄4 |
|
(b) A percentage |
(b)15⁄20 = 75⁄100 = 75% |
|
2. Two people divide $80 in the ratio 3 : 7 How much does each person get? |
2. The ratio 3 : 7 means a total of 10 parts. Each part is $80 ÷ 10 = $8 The first person gets: 3 × $8 = $24 |
Proportion
Two sets of numbers are in direct proportion when the ratio between corresponding members of the sets is the same.
e.g. A = {3, 6, 9} is in proportion to B = {12, 24, 36} because members of set B are 4 times the size of the corresponding members of set A.
Problems involving Proportion
Problems involving proportion can be solved in two ways:
|
Method 1
|
Method 2
|
|
Find the value of one of the units being used. |
Form an equation involving corresponding ratios. |
|
A driver uses 10 litres of petrol to cover 80 km. How much petrol would be used to cover 200 km? |
A driver uses 10 litres of petrol to cover 80 km. How much petrol would be used to cover 200 km? |
|
80 km would require 10 litres. 1 km would require 10⁄80 litres. 200 km would require 10⁄80 × 200 litres. 25 litres would be required. |
Let x be the amount of petrol needed.
|
Rates
A rate compares two quantities of a different kind.
Rates can be shown on graphs. See Topic 40.
e.g. Speed = kilometre per hour ![]()
For exciting and fun practice with speed, distance, time and bearings − ![]()
Wage rate = Dollars per week ![]()
|
A woman earns $425 in 50 hours. |
Rate of pay = 425⁄50 = $8.5/hour |
|
A motorist travels 85 km in 2 hours. |
Speed = 85⁄2 = 42.5 km/hr
|