1. Sketch the following vectors and use Pythagoras' Theorem to find the length (magnitude) of each to 2 significant figures:
![]()
2. Give the matrix (bracket) form of the following vectors. Each square is one unit.

|
(a) |
(b) |
(c) |
(d) |
3. Draw the following vector triangles and write down the resultant vector:
|
(a) |
(b) |
(c) |
(d) |
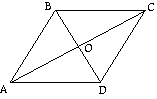
4. ABCD is a parallelogram.
|
(a) Give a vector equal to (b) Complete (c) True or false? (d) Complete (e) Complete
|
|
|
5. The figure shows the vector Copy and complete a vector triangle to illustrate the vector sum:
|
|
|
6. A plane sets off on a couse of 090° (East) at a speed in the air of 300 km/h. A wind of speed 50 km/h is blowing from the south (180°). a. Draw a vector triangle to show the actual path of the plane. b. Use a scale drawing to find the bearing of the planes flight. |
|
|
7. |
A cyclist can pedal downhill at 35 km/h He is cycling down a straight mountain road in a southerly direction. The wind is blowing from the west at 10 km/h. Draw a vector diagram to illustrate this and then use it to find the cyclist's actual speed. |
|
8. Ron the runner runs in a marathon and is heading due North. His speed in still air is 15 km/h. He has the wind behind him from the South at a speed of 5 km/h. What would his actual speed be? |
|
|
9. |
Jung-Min is a swimmer and is swimming from Mission Bay in Auckland to Rangitoto Island. He can swim at 3 km/h in still water. The current is directly from the side and is 1 km/h. Draw a vector traingle to scale and a scale drawing to find his swimming speed. |
|
10. A windsurfer does the same trip as Jung-Min in question 9. On a windy day for her journey the wind is directly behind and blowing at 25 km/h and the current is directly from the side at 4 km'h. Draw a vector triangle and a scle drawing to find her speed. |
|