Year 8 (NZ Y9) Quiz
Click on the question you wish to answer, in any order:
Red questions are about ARITHMETIC
Blue questions are about GEOMETRY
Green questions are about ALGEBRA
Orange questions are about MEASUREMENT
Purple questions are about STATISTICS
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
104 |
105 |
106 |
107 |
108 |
109 |
110 |
111 |
112 |
113 |
114 |
115 |
116 |
117 |
118 |
119 |
120 |
121 |
122 |
123 |
124 |
125 |
126 |
127 |
128 |
129 |
130 |
131 |
132 |
133 |
134 |
135 |
136 |
137 |
138 |
139 |
140 |
141 |
142 |
143 |
144 |
145 |
146 |
147 |
148 |
149 |
150 |
151 |
152 |
153 |
154 |
155 |
156 |
157 |
158 |
159 |
160 |
161 |
162 |
163 |
164 |
165 |
166 |
167 |
168 |
169 |
170 |
171 |
172 |
173 |
174 |
175 |
176 |
177 |
178 |
179 |
180 |
181 |
182 |
183 |
184 |
185 |
186 |
187 |
188 |
189 |
190 |
191 |
192 |
193 |
194 |
195 |
196 |
197 |
198 |
199 |
200 |
*If you need help on a particular question, click on the HINT button
Question 1. How many sides does an octagon have?
A hexagon has 6 sides and an octagon has more!
A octagon has 8 sides.
Question 2. Calculate 3 x 10 + 6 x 5
Remember BEDMAS
30 + 30 = 60
Question 3. Evaluate 5x + 3 if x = −2
5 x −2 = ? A positive or negative number?
−7
Question 4. What is the sum of the interior angles of a triangle?
A square is made up of two triangles. How many degrees in a square? Now half it!
180°
Question 5. How many sides does a rhombus have?
A rhombus is a "squashed" square.
Four
Question 6. Calculate 8 + 6 x 2 + 4
Remember BEDMAS
24
Question 7. List the prime numbers between 10 and 20.
Prime numbers have only two factors. THemselves and 1. e.g. 23
11, 13 ,17 and 19
Question 8. How many centimetres in 1.3 metres?
There are 100 centimetres in a metre.
130 cm
Question 9. What is the product of 4 and 5?
Product means "multiply"
20
Question 10. Solve 2x − 6 = 12
To get started, add 6 to both sides of the equation.
x = 9
Question 11. What is 0.4 as a fraction in its simplest form?
The 4 is in the "tenths" column.
4/10 = 2/5
Question 12. How many axes of symmetry does a rectangle have?
Think carefully - are the diagonals axes of symmetry?
A rectangle has two axis of symmetry
Question 13. A clock loses 15 minutes every day. How many minutes would it lose over a year? (Not a leap year)
There are 60 minutes in an hour and 365 days in a year.
5475 minutes
= 91.25 minutes
Question 14. A meal for 5 people uses 10 eggs. How many eggs are needed if the meal is to be made for 20 people? 
How many eggs would ONE person need? OR How many times does 5 go into 20?
5 eggs are needed
Question 15. How many axes of symmetry does a regular hexagon have?
How many sides does a regular hexagon have?
Six sides and six axes of symmetry
Question 16. What is the image of the point (3,2) after a reflection in the x-axis?
Draw a set of x-axis and y-axis and mark the point (3,2) then carry out the change.
(3, −2)
Question 17. How many square centimetres is the surface area of a cube of side 1 cm ?
Find the area of one face of the cube. Now work out how many faces a cube has.
6 square centimetres
Question 18. Write 6.3 x 102 as an ordinary number.
For a POSITIVE index move the decimal point to the RIGHT.
630
Question 19. What is the direction E as a bearing ?
Remember that NORTH is 0° and direction is measured CLOCKWISE.
90°
Question 20. Write the fraction 82/100 as a decimal?
The HUNDREDTHS column is the second one to the right of the decimal point.
0.82
Question 21. Expand 2(3x + 5)
Multiply 2 by 3x then 2 by 5
6x + 10
Question 22. Expand 8(2x − 3)
Multiply 8 by 2x then 8 by −3
16x − 24
Question 23. What is 10% of 230?
Quick way: 10% is one tenth. i.e. Divide 230 by 10
230 x 0.1 = 23
Question 24. How many one litre cans of paint would you need to buy to paint a wall 3 metres by 7 metres with a coat of of paint if each can of paint covers 30 000 cm2?
First find the area of the wall Remember that 1 m2 = 10 000 cm2
Seven cans of paint would be needed
Question 25. Simplify 4a x 5b
Multipy numbers first and then the variables.
20ab
Question 26. Which is the solution for the equation 2x + 6 = 10
Subtract 6 from both sides then divide both sides by 2.
x = 2
Question 27. What name is given to the line AB, if it were to pass through the centre of a circle?

AB is a chord, if it passes through the centre it is a _ _ _ _ _ _ _ _.
AB would be a diameter
Question 28. A rain guage indicates a rainfall of 26 mm. What is this rainfall in centimetres ?
There are 10 mm in 1 cm
2.6 cm
Question 29. Calculate 3 + 4 x 2 − 3
Multiply first
8
Question 30. Calculate 44
Do NOT multiply 4 by 4 !!!!
256
Question 31. What is the value of 23?
Don't do 2 x 3!
8
Question 32. Express 6 as a percentage of 30.
Write 6 out of 30 as a fraction i.e. 6/30
and now change to a percentage by multiplying by...
20%
Question 33. If x = 4, what is the value of 2x2?
Remember that squaring comes before multiplying by 2
32
Question 34. If a = 2 and b = 4 what is the value of 3ab ?
Multiply 3 by 2 by 4 Easy!
24
Question 35. Calculate (5.2 x 102) + (4.5 x 102)
What is 102? Then work out each bracket before adding. (On a calculator use the EXP button)
970
Question 36. Lengths of wood of 27 cm, 59 cm and 63 cm are cut from a piece 2 metres long. What length of wood remains?
Add together the lengths of the bits that are being cut off.
200 − 149 = 51 cm
Question 37. Is -2 a whole number or an integer?
Whole numbers start at 0
-2 is an integer.
Question 38. If a = 5 and b = −6, what is the value of 2ab ?
Substitute the numbers and then multiply the three things together.
2 x 5 x −6 = −60
Question 39. Solve the equation 3x + 4 = 22
Subtract 4 from both sides then divide both sides by 3.
x = 6
Question 40. What is the area, in square metres, of a rectangle whose sides have been measured at 50 cm and 1.5 m?
Change the 50 cm into metres and then multiply the two lengths.
0.75 m2
Question 41. What is the square of 3.5?
"To square a number you multiply it by itself."
12.25
Question 42.A six-sided dice is thrown
What is the probability that a number greater than a 4 comes up?
How many numbers on a six-sided die are greater than 4?
Probability = 1/3
Question 43. Solve x2 = 9
Careful! There are two answers
x = 3 or −3
Question 44. Calculate 21 − 5 x 3
Do the MULTIPLYING first!!!!
6
Question 45. What is the value of 202?
"To calculate something by the power of 2, you multiply it by itself."
400
Question 46. What is the volume of the cube with side length 3 cm?
The volume of a cube or cuboid is length x width x height In a cube these are all the same.
Volume = 3 x 3 x 3 cm3 = 27 cm3
Question 47. Express 60% as a decimal.
60% means 60/100
0.60 = 0.6
Question 48. Increase $60 by one third of its value.
To find one third of anything divide it by 3
$80
Question 49. Express 50 as a percentage of 200.
Calculate 50 ÷ 200 and then multiply by 100
25%
Question 50. Give the formula for the surface area of a cube length L.
How many faces does a cube have? The area of each face will be the same
6L2
Question 51. What is the square root of 4900?
(Work it out without your calculator!)
You could write 4900 as 49 x 100
70
Question 52. Evaluate 32 x 32 ?
Square each number first then multiply them together.
9 x 9 = 81
Question 53. A square has a perimeter of 48 cm. How many square centimetres in its area ?
"If the perimeter of a square is 48, how long are each of its equal sides?"
144 cm2
Question 54. Each interior angle of a regular polygon is 120°.How many degrees is each exterior angle?
The interior angle and the exterior angle are the only two angles on the same straight line, so what do they add up to?
180 - 120 = 60°
Question 55. How many sides does a parallelogram have?
A parallelogram is a quadrilateral with two pairs of opposite parallel sides and opposite angles are equal.
4 sides
Question 56. Evaluate (find the value of)
15 − 5 + 15
Work from left to right.
25
Question 57. If a house costs $250,000 and it increases in one year by 10%, what will its new value be?
Find 10% of $250,000 and add it on OR Multiply $250,000 by 1.10
$275,000
Question 58. Decrease a salary of $100,000 by 20%
Multiply the amount by 0.8 (100 - 20)/100 OR Work out 20% of $100,000 and subtract it.
$80,000
Question 59. Find x 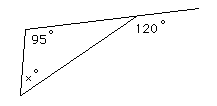
Use the rule that begins "The exterior angle of a triangle equals the sum of..."
25°
Question 60. If a = 6, b = 2 and c = 3 evaluate a2bc
Work out a2 first
216
Question 61. Write 5 thousandths as a decimal?
Put a "5" into the thousandths column.
0.005
Question 62. The length of a netball court is twice its width. If its perimeter is 180 metres how long is the court?
Trial and error
OR
use the formula P = 2L + 2W
60 metres
Question 63. The length of a rugby is twice its width. If its length is 100 metres what is its perimeter
Find the width by halving the length. Then add the four lengths together.
300 metres
Question 64. How many grams in two and a half kilograms?
There are 1000 grams in 1 kilogram.
2500 g
Question 65. Calculate 4 x 5 + 6 − 3
"Remember BEDMAS!"
23
Question 66. Two of the angles in a triangle are 59° and 73°. What is the size of the other angle?
The inside angles of a triangle add up to 180°
48°
Question 67. What is the mean (average) of the numbers 3, 5, 10, 12, 20?
The mean is the SUM of all of the values divided by the NUMBER of values.
mean = 50/5 = 10
Question 68. My friends and I share a Lotto jackpot of $480. There are 7 other people in the syndicate. How much did each of us win?
Read the question carefully. How many people are there altogether?
$60
Question 69. How many minutes are there between 1.30 pm and 3.20 pm on the same day?
Remember there are TIMES and not DECIMAL numbers. (There are 60 minutes in an hour!)
110 minutes
Question 70. $30 is shared between two people in the ratio 2 : 1. Jim gets the largest share. How many dollars does he get?
How many "parts" are there altogether?
$20
Question 71. Two 300 g weights are added to a 600 g weight. Express the total weight in kilograms.
"There are 1000 grams in a kilogram."
1.2 kg
Question 72. How many sides does a regular polygon with exterior angles of 60° have?
The EXTERIOR angles of ANY polygon add up to 360°.
360/60 = 6 Therefore there are 6 sides.
Question 73. What is 25% of 30?
Either use the fact that 25% is the same as a quarter OR Multiply 30 by 0.25
30 x 0.25 = 7.5
Question 74.What name is given to an angle that is less than 90°?
Choose from: acute, reflex and obtuse
Acute angles are less than 90°
Question 75. If it takes 5 hours to drive 450 km, what speed is this in kilometres/hour?
Speed = Distance/Time
90 kilometres/hour
Question 76. If a car travels 315 km at an average speed of 90 km/hour, how long will the journey take?
Time = Distance / Speed
3.5 hours
Question 77. What is the square root of 121?
"What? x What? = 121!"
11
Question 78. Factorise 80x + 70
Is there a COMMON factor?
10(8x + 7)
Question 79. What is the next prime number after 19?
Prime numbers have only themselves and 1 as factors.
23
Question 80. How many cm2 are there in 2 m2?
There are 10 000 cm2 in 1 m2
20 000 cm2
Question 81. Calculate 2.12
To "square" a number multiply if by itself.
4.41
Question 82. What is the percentage increase if $200 is increased to $240?
% increase = amount of increase x 100 original amount
40/200 x 100 = 20%
Question 83. How many two digit numbers can be made using the digits 4, 5 and 6?
How many ways can you fill the first digit and how many ways can you fill the second digit? Remember both digits can be the same.
There are 9 ways from 44 through to 66
Question 84. Evaluate (−3)3
Calculate ≄3 x ≄3 x ≄3 Care with the signs!
≄27
Question 85. What type of angle is 67°? Choose from acute, obtuse and reflex.
You've been given a clue already!
Acute angle
Question 86. What is 50% of 210?
What FRACTION is 50% OR Multiply 210 by 0.5
105
Question 87. $360 is divided among 2 friends in the ratio 4:5 What is the biggest share?
There are 9 parts altogether so divide 360 by 9. The biggest share will be 5 of those parts.
$200
Question 88. Calculate (100 + (100 + (100 + (100 + 100))))
Start from the inside bracket and work out.
500
Question 89.Two angles are congruent. One of them is 67°, what is the size of the other?
No clues, too easy!
67°
Question 90. Solve the equation 2x + 4 = 16
Subtract 4 from both sides and then divide both sides by 2.
x = 6
Question 91. How many vertices does a triangular prism have?
The vertices are the corners of the prism.
A triangular has 6 vertices.
Question 92. What is the median of {6, 8, 7, 5, 5} ?
The median of a set of numbers is the middle number when they are arranged in order.
The median is 6
Question 93. How many g in 2.5 kg?
There are 1000g in 1kg
2500 grams
Question 94. What is the surface area of a cuboid with sides 5 cm by 6 cm by 7 cm?
When working out the surface area of the cube remember there are 6 faces to consider.
214 square centimetres
Question 95. Solve the equation 3x − 5 = 10
Add 5 to both sides and then divide both sides by 3
x = 5
Question 96. A cake contains 10% sugar. How many grams of sugar are there in a 3 kg cake ?
To find 10% of a quantity multiply it by 0.1. Remember there are 1000 g in 1 kg
300 grams of sugar
Question 97. How many metres in 8.4 kilometres ?
There are 1000 metres in one kilometre.
8400 metres
Question 98. Which is the bigger? 4 g or 300 mg
There are 1000 mg in a g
3g is heavier!
Question 99. 10 pieces of wood of the same size are stacked on top of each other. The stack is 1.8 metres high. What is the thickness (in cm) of each piece of wood ?
There are 100 cm in 1 m
Each piece of wood is 18 cm thick.
Question 100. True or false? (0.1)4 = 0.001
You don't even need to get your calculator out for this one
0.1 x 0.1 x 0.1 x 0.1 = 0.0001 so the statement is false.
Question 101. Simplify 8x − 3x + 4x − 5x
Work from left to right.
4x
Question 102. Write 8.4 correct to the nearest whole number.
Is 4.4 closer to 8 or 9 on the number line?
8
Question 103. What is the order of rotational symmetry of a rectangle?
Rotational symmetry is the number of times a shape fits into itself when rotated about its middle.
2
Question 104. Simplify 4a x 5b
Multiply the numbers first and then the variables (letters). (Leave variables in alphabetical order)
20ab
Question 105. If y= 3x + 5
What is the value y when x = 2?
After substituting x = 2
y = 3 x 2 + 5 Work it out!
11
Question 106. If x = −4, what is the value of x2?
What is a negative number multiplied by a negative number? Positive or Negative?
16
Question 107. What is the area of a rectangle of size 3 cm by 4 cm if it is enlarged by a scale factor of 2?
Double the length of each side and then multiply them together to find the area.
48 square cm
Question 108. Simplify 4 + p + p − p + 3
Add the numbers and then add and subtract the pees!!
7 + p
Question 109. Solve the equation n + 13 = 23?
Subtract 13 from both sides.
n = 10
Question 110. What is the probability of throwing a 2 or a 4 when a six-sided die is thrown?
Write 2 out of 6 as a fraction in its simplest form.
2/6 = 1/3
Question 111. What is the probability that a day of the week, chosen at random, begins with an S?
Write the answer as a fraction with a denominator of 7
2/7
Question 112. What is the area of the triangle? 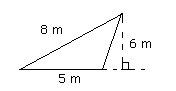
Area of triangle = 0.5 x base x height
Area = 15 m2
Question 113. What is the surface area of a solid cuboid of dimensions 3 cm by 8 cm by 6 cm?
Remember a cuboid has 6 faces.
180 cm2
Question 114. What is the value of x if the three inside angles of a triangle measure 65°, 57° and x°?
The angles of a triangle are SUPPLEMENTARY (they add up to 180°).
58°
Question 115. What name is given to an equal-sided triangle?
Choose from scalene, isosceles or equilateral triangle.
Equilateral triangle
Question 116. Write 8.37 x 102 as a whole number
Move the decimal point two places to the ...
837
Question 117. Calculate (4.2 x 10) + (3.5 x 100)
Work out the two brackets first.
392
Question 118. How many sides of equal length does a scalene triangle have?
An equilateral triangle has 3 equal sides, an isosceles triangle has 2 equal sides and a scalene triangle has...
... no equal sides.
Question 119. How many mm in 3.5 cm?
1 cm = 10 mm
3.5 cm = 35 mm
Question 120. How many axes of symmetry does a rhombus have?
Axes of symmetry are mirror lines drawn through the shape.
Only 2, the diagonals
Question 121. A clock gains 15 seconds every day. How many minutes will it gain over a year? Give the answer to the nearest minute. (Not a leap year!)
There are 365 days in normal year. There are 60 seconds in a minute.
91 hours
Question 122. Write 3/5 as a decimal.
Either: Divide 3 by 5 or Change the fifths to tenths
0.6
Question 123.The length of a rectangle is twice its width. If its perimeter is 60 cm what is its area?
Draw a diagram. Let the width be x so the length will be 2x. Form an equation for the perimeter
200 cm2
Question 124. How many of axes of symmetry does an isosceles triangle have?
An isosceles triangle is a triangle with two sides of equal length.
One axis of symmetry
Question 125. Is 39 a prime number?
Does it have any factors apart from 39 and 1?
No, it is not a prime number! 3 and 13 are factors as well as 1 and 39.
Question 126. Find a positive solution to the equation
3a + 9 = 45
Subtract 9 from both sides and then divide by 3.
a = 12
Question 127. What is a speed of 50 km/hr in m/s? (Give answer to nearest metre per second.)
Multiply by 1000 to change it to metres then divide by 60 x 60 to change the hours to seconds
14 m/s (to nearest metre)
Question 128. 135 minutes + 225 minutes is equal to how many hours?
Add the two numbers and then divide by 60 to change to hours.
6 hours
Question 129. If a bike costs $400 without GST at 12.5%, how much is it with GST (to nearest cent)?
Multiply by 9 and divide by 8 (i.e. 112.5/100)
$450
Question 130. How many cm2 are there in 3.2 m2?
1 m2 = 10 000 cm
32 000 cm2
Question 131. Solve 3(2x + 5) = 21
Expand the brackets first and subtract 15 from both sides...
x = 1
Question 132. Simplify 2p + 2 x 7p
Remember that BEDMAS applies to algebra too. Multiply before adding.
16p
Question 133. Calculate 3.23 (without using a calculator)
3.23 means 3.2 x 3.2 x 3.2
32.768
Question 134. Give the bearing equivalent to the compass direction of South.
North is a bearing of 000°
180°
Question 135. Find the value of 3x2 if x = 2
Remember BEDMAS. Squaring comes first!
12
Question 136. What is the MEDIAN of {8, 6, 7, 3, 7, 5, 5} ?
The median is the MIDDLE number when you arrange them in order.
Median = 6
Question 137. Calculate 3 − (3 − (3 − 3))
Start from the innermost brackets.
0
Question 138. How many axes of symmetry does a rhombus have?
Axes of symmetry are mirror lines.
A rhombus has 2 axes of symmetry. Note that the diagonals are NOT axes of symmetry.
Question 139.What is the surface area of a cube of side 5 cm?
How many surfaces (square faces) does a cube have?
6 faces at 25 cm2 each = 150 cm2
Question 140. Solve the equation 4x − 13 = 35
Add 13 to both sides and then divide by 4.
x = 12
Question 141. Which points are invariant i.e. Don't change, under a reflection in the x-axis?
Invariant means that they do not move.
All points on the x-axis don't change so the answer is that the x-axis is invariant.
Question 142. A car uses 10 litres of petrol to travel 175 km. How many kilometres does it travel on 1 litre?
Divide by 10
17.5 km/L
Question 143. Which is the smallest: three twentieths, four twenty-fifths, or fourteen hundredths?
Change each fraction to hundredths
Fourteen hundredths
Question 144. Calculate 8 + 4 x 3 − 5
Remember BEDMAS. Multiply before Adding or Subtracting
15
Question 145. What is 3.7 cm + 4.5 cm rounded to the nearest cm?
Add the two measurements and then decide which whole number the answer is closest to.
8 cm
Question 146. How many hours are there in four weeks?
How many hours in a day? How many day in a week?
672 hours
Question 147. Solve 5(x − 4) = 15
Expand the brackets and then take x terms to one side and numbers to other.
5x − 20 = 15 5x = 35 x = 7
Question 148. How many minutes are there between 5.45 pm and 6.23 pm on the same day?
Remember there are 60 minutes in an hour.
38 minutes
Question 149. How many edges does a cube have?
Edges are where two faces meet.
A cube has 12 edges.
Question 150. What is the next prime number after 23?
Prime numbers have only themselves and 1 as factors.
29
Question 151. A triangle has a base of 7 cm and a perpendicular height of 6 cm. What is its area?
Area of triangle = 0.5 x base x height
Area = 21 cm2
Question 152. How many multiples of 3 are there BETWEEN 30 and 40?
Multiples of 4 are numbers such as 24, 27 ,30 etc.
There are 3 multiples of three between 30 and 40: 33, 36 and 39.
Question 153. If 100 books cost $800.00 What would 30 books cost?
Find the cost of ONE book first by dividing and then...
30 books would cost $240
Question 154. How many faces does a square-based pyramid have?
A face is a flat surface.
A square-based pyramid has 5 faces.
Question 155. What is the highest common factor of 18 and 24?
List all of the factors of each number and then find the largest. (A FACTOR is a number that divides into another without a remainder.)
H.C.F is 6.
Question 156. What is the mean of {6, 8, 7, 5, 4}?
The mean is the average. To work it out, add all the numbers together and then divide by 5 (because there are 5 numbers).
The mean is 6
Question 157. 16 kilograms = ....... g
The prefix "kilo" means a thousand.
16 000
Question 158. How many degrees do the interior angles of an isosceles triangle add up to?
The interior angles of ANY triangle always add up to ...
180°
Question 159. To dig a tunnel 40 m long, 2 m wide and 2 m high, how much earth, in cubic metres would have to be removed ?
Volume of a rectangular prism = length x width x height
160 m3
Question 160. Find x if 3x + 4 = 7
Subtract 4 from both sides of the equation then divide both sides by 3.
x = 1
Question 161. What is the area of a rugby field 105 m by 60 m?
Area of a rectangle = length x width
6300 m2
Question 162. To fill a rectangular-shaped pool 20 m long, 10 m wide and 2 m deep, how much water, in litres, would have to be used?
1 m3 = 1000 litres
400 000 litres of water would be needed.
Question 163. What is the lowest common multiple of 4 and 5 ?
Write out the multiples of 4 and 5 and find the lowest common one.
20 is the LCM of 4 and 5
Question 164. How many vertices? 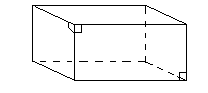
Vertices is the plural of vertex which means "corner".
There are 8 vertices in a cuboid.
Question 165. Factorise 8y + 4x + 12
Are there any common factors?
4(2y + x + 3)
Question 166. What size are the two smallest angles of a right-angled isosceles triangle?
One of the angles in the triangle is 90° So what do the other two equal angles add up to? Now divide this by 2
45°
Question 167. How many centimetres are there in 2.5 kilometres?
There are 100 centimetres in 1 metre and 1000 metres in 1 kilometre.
There are 250 000 cm in 2.5 kilometres.
Question 168. Expand and simplify 5p − 2(p − 3)
What effect does the negative sign OUTSIDE the bracket have on the negative sign INSIDE the bracket?
5p − 2(p − 3) = 5p − 2p + 6 = 3p + 6
Question 169. Evaluate 3 + 3 x 32
Remember BEDMAS! Do that exponent first!
30
Question 170. What is the value of x if 5x2 is 80?
Divide 80 by 5 and then work out what x2 has to be.
x = 4
Question 171. Expand (2x + 3)(x − 7)
There should be three terms in the final answer.
2x2 − 11x − 21
Question 172. Solve 2(x + 3) − 3(x − 2) = 3(2 − x)?
You'd better expand the brackets first and then take all of the x terms to one side of the equation and all of the number to the other side.
x = −3
Question 173. Two of the interior angles of a cyclic quadrilateral are 103° and 21°. What is the size of the other two angles?
The interior opposite angles of a cyclic quadrilateral add up to 180°
77° and 159°
Question 174.For what two angles between 0° and 360° is the tangent ratio undefined?
Think of where the dotted, vertical lines are on the tangent graph.
90° and 270°
Question 175. If a straight line has a gradient of 2, what is the gradient of its perpendicular bisector?
It will be flatter (a smaller number) and it will be a negative gradient.
−0.5
Question 176. What is the upper quartile of the numbers 3, 4, 6, 1, 2, 5, 6, 3, 9, 5, 6, 2, 4, 3?
Arrange them in order then split the numbers into 4 sets
Upper quartile is 6
Question 177. What is the size of the interior angles of a regular octagon?
The OUTSIDE or EXTERIOR angle is 360/8.
135°
Question 178. Simplify 6p = 2(p − 3)
Expand the brackets first.
p = −1.5
Question 179. Evaluate 4 − −3 − 32
Remember that when you minus a negative it is equivalent to adding a positive. Strange but true!
−3
Question 180. What is the size of each exterior angle of a regular hexagon?
The sum of the exterior angles of ANY polygon is 360° and in a hexagon there are 6 of them.
60°
Question 181. True or false?
−2 + −4 x 5 = −30
Apply the BEDMAS rule.
FALSE! The left hand side comes out to be −22
Question 182. The size of each exterior angle of a regular polygon is 24 degrees. How many sides does the polygon have?
The exterior angles of ALL polygons always add up to 360°
The polygon has 360/24 = 15 sides
Question 183. Factorise 3x2 + 6x
Look for the common factor
3x(x + 2)
Question 184. A 405 gram can of pears costs $1.20, while a 125 gram can of the same fruit costs $0.40. Which is better value?
By division, work out the cost of 1 g of pears for each can.
The 405 gram can is better value.
Question 185. Two students toss a coin at the same time. What is the probability that neither of the coins comes up heads?
If neither of the coins is a head, what must they both be!
P(Tail,Tail) = 0.5 x 0.5 = 0.25
Question 186. Bill spends two thirds of his money at the movies and a half of what is left on his lunch. What fraction of his money remains?
When he spends two thirds, what fraction is left?
1/6
Question 187. Find the value of x 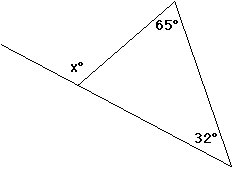
The exterior angle of a triangle equals the sum of the two interior opposite angles.
x = 97°
Question 188. Find the two solutions to the equation
x2 + 4x − 5 = 0
Factorise it first!
x = −5 or +1
Question 189. Change 240 000 cm3 into m3.
There are 100 x 100 x 100 cubic cemtimetres in a cubic metre.
0.245 m3
Question 190. The mean of a golfer's first 5 rounds of the season is 73 strokes. How many strokes would she need on her next round to bring her average down to 72?
What total is needed on 6 rounds to average 72?
She would need a round of 67 strokes!
Question 191. Give the largest number that is a multiple of 4 and also a factor of 24.
List the factors of 24 and list the multiples of 4. Then find the biggest!
24
Question 192. Find the size of the biggest angle in the quadrilateral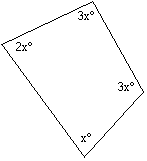
How many x are there? What is the total number of degrees in a quadrilateral?
9x = 360
x = 40
The biggest angle is 3x = 120°
Question 193. Solve the equation x + 2 + 3x + 6 = 12
Simplify the left hand side of the equation first.
x = 1
Question 194. The are of a square is 144 cm2. What is its perimeter?
What x What = 144???
The perimeter would be:
4 x 12 = 48 cm
Question 195. The probability of passing an examination is estimated at 0.55. If 1000 people sit the examination how many would you expect to pass?
Expected value = Number of people x Probability of not passing
550 would be expected to pass.
Question 196. Write 3.65 x 102 as an ordinary number.
102 = 100
365
Question 197. In a triangle there are three angles A, B and C . A is 65° and B is 75°. What is the size of angle C?
The angles in a triangle add up to 180°
40°
Question 198. Factorise 4x − 48
Is there a common factor? i.e. A number that divides into both 4x and 48.
4x − 48 = 4(x − 12)
Question 199. Write 3 500 g in kg
There are 1000 grams in 1 kilogram.
3 500 g = 3.5 kg
Question 200. What is the mean of the following amounts:
$3, $2, $4, $3, $5 and $7?
To get the mean of six amounts of money, add the six amounts together and then divide by 6.
Mean = $4