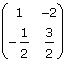Matrices form a mathematical system with operations such as multiplication and addition.
Commutativity
In general, the multiplication of 2 X 2 matrices is NOT commutative. i.e. The order in which the matrices are multiplied is important.
Example
If A =
and B =
then
AB =
=
BA =
=
Showing that AB ≠ BA.
The same applies to matrix subtraction A − B ≠ B − A.
Matrix subtraction is NOT commutative.
Matrix addition is commutative A + B = B + A.
Associativity
Matrix multiplication is associative. i.e. The grouping of the matrices is not important when multiplying.
Example
If P =
, Q =
, R =
Showing the P(QR) = (PQ)R
Identity Matrix
The identity 2 X 2 matrix for addition is ![]() .
.
e.g.
The identity 2 X 2 matrix for multiplication is ![]()
e.g.
Inverse Matrix
Addition The inverse 2 X 2 matrix for addition is obtained by changing the signs of each element.
e.g. If A =
, the additive inverse is
A matrix and its inverse combine to give the identity matrix.
e.g.
Multiplication The inverse 2 X 2 matrix for multiplication is obtained by:
- Exchanging the elements of the leading diagonal.
- Changing the signs of the elements of the other diagonal.
- Multiplying the resulting matrix by

In general terms, if A = ![]()
the inverse A-1 = ![]()
|
Example If B = The inverse of B, B-1 = B-1 = |
A matrix and its inverse combine to give the identity matrix.
e.g. B x B-1 = I
Solving Simultaneous Equations using Matrices
In addition to the four methods mentioned in an earlier topic, simultaneous equations can also be solved using matrices. The method involves writing the equations in matrix form and then multiplying each side by the inverse matrix to obtain the identity matrix.
The example below is used to solve the simultaneous equations:
2x + 3y = 5
x + 2y = 1
| Method | Example |
| Step 1: Set up the equations in matrix form. | |
| Step 2: Pre-multiply each side by the inverse 2 X 2 matrix. | |
|
Step 3: Evaluate the matrix products. |
The solution set is {(7, -3)} |