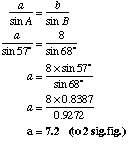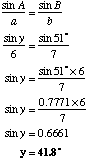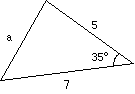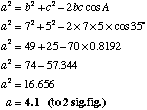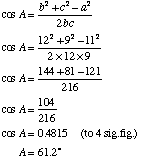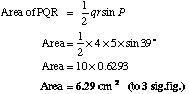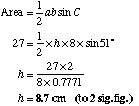The trigonometric methods given earlier apply only to triangles containing a right angle.
For triangles without a right angle, the sine rule, the cosine rule and the area formula can be used to solve triangles and find their areas.
New Zealand students, please note that this topic is now assessed at NCEA, Level 2 (NZ Year 12).
Sine Rule
The sine rule is concerned with triangles where pairs of angles and their opposite sides are given.
The sine rule states:
|
|
 |
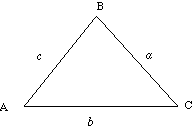or, in an alternative form for use when finding angle sizes:
|
(a) Find the value of a  |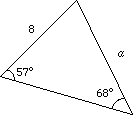
Use the formula: |
|
(b) Find the size of angle y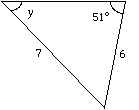 
|
Use the formula: ( to 1 d.p.) |
Cosine Rule
The cosine rule is concerned with triangles where the lengths of two sides and the angle between them, or the lengths of three sides, are given.
The cosine rule states:
|
or , in alternative form for finding angles:
|
 |
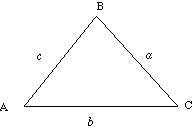(a) Find the value of a
|
Use the formula: |
|
(b) Find the size of angle BAC  |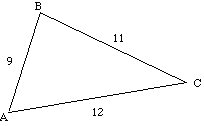
Use the formula: (to 1 d.p.)
|
Area Formula
The area of a triangle can be found given the lengths of two sides and the angle between them.
The area formula states:
|
Area of triangle = |
 |
|
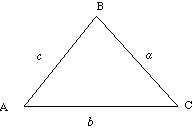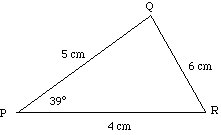
(a) Find the area of
|
|
|
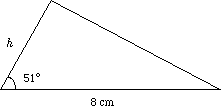
(b) The area of the triangle is 27cm2. Find the value of h.
|
|
PQR
