Ratio
A ratio compares two quantities of the same kind.
Example
In my class there are 8 girls and 12 boys. The ratio of girls to boys is 8 : 12. This ratio simplifies to 2 : 3
Before simplifying a ratio, each quantity should be in the same units.
e.g. $5 to $3
60 minutes to 30 minutes
A ratio can be expressed in several forms.
e.g. A ratio of 1 to 2 can be written 1 : 2 or
or 50%
Ratios can be simplified like fractions.
e.g. 20 : 40 = 10 : 20
10 : 20 = 5 : 10
5 : 10 = 1 : 2
|
1. Write the ratio 15 : 20 as: |
|
|
(a) A fraction |
(a) |
|
(b) A percentage |
(b) |
|
2. Two people divide $80 in the ratio 3 : 7 How much does each person get? |
2. The ratio 3 : 7 means a total of 10 parts. Each part is $80 ÷ 10 = $8 The first person gets: 3 × $8 = $24 The second person gets: 7 × $8 = $56 |
Proportion
Two sets of numbers are in direct proportion when the ratio between corresponding members of the sets is the same.
e.g. A = {3, 6, 9} is in proportion to B = {12, 24, 36} because members of set B are 4 times the size of the corresponding members of set A.
Problems involving proportion can be solved in two ways:
Method 1. Find the value of one of the units being used.
Method 2. Form an equation involving corresponding ratios.
|
Example 1 Method 1 |
Method 2 |
|
A driver uses 10 litres of petrol to cover 80 km. How much petrol would be used to cover 200 km?
|
A driver uses 10 litres of petrol to cover 80 km. How much petrol would be used to cover 200 km?
|
|
80 km requires 10 litres. 1 km would require 200 km would require 25 litres would be required. |
Let x be the amount of petrol needed.
|
litres.
.
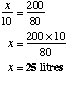25 litres would be required.
