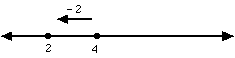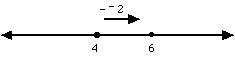Sets
Although set theory and operations are not now included in this course it is useful to know what a set is, and about the various number sets.
Notation
A set is a collection of objects. These objects, called the members or elements of the set, are enclosed in braces {...} and separated by commas.
A set can be described in words: A = { the first three natural numbers}
or by listing each member: A = {1, 2, 3}
Number sets
The numbers we use can be chosen from several sets.
- The set of natural numbers.
-
N = {1, 2, 3, 4, ...}
-
The set of whole numbers.
W = {0, 1, 2, 3, ...}
-
The set of integers.
I = {... -2, -1, 0, 1, 2, 3,...}
-
The set of rational numbers
Q =

e.g.
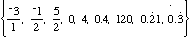
-
The set of irrational numbers
Irrational numbers are numbers that cannot be written as rational numbers.
e.g. {infinite, non-recurring decimals}
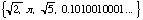
-
The set of real numbers (rational numbers + irrational numbers)
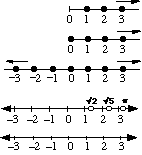
Number lines
The number sets can be shown on number lines.
|
Natural numbers, N (excludes zero) Whole numbers, W (includes zero) Integers, I (positive and negative whole numbers) Rational numbers (all except irrationals) Real numbers, R (all numbers) |
 |
Integers
The integers are the positive and negative numbers and zero.
For practice with integer calculations ![]()
Addition
Use a number line when adding and subtracting integers. The first integer is the starting point on the number line.
- When adding a positive integer, move to the right.
e.g. 4 + 2 = 6
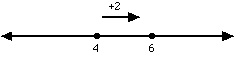
-
When adding a negative integer, move to the left.
e.g. 4 + − 2 = 2
Subtraction
- When subtracting a positive integer, move to the left.
e.g. 4 − 2 = 2
- When subtracting a negative integer, move to the right
e.g. 4 − − 2 = 6
Multiplication and division
The rule is the same for both multiplying and dividing two integers.
The table illustrates these rules:
Examples: