The logarithmic function is the inverse of the exponential function.
The inverse of y = ex is y = log ex (which is written as ln x and called a natural logarithm ).
On a calculator the loge button is 
.
The gradient function of y = ln x can be seen by looking at the graphs of the two functions.
By looking at the gradients at x = 2 and x = 3 if would seem to indicate that the gradient function of
y = ln x is y ' = 
.
|
If f(x) = ln x then f '(x) = 1⁄x |
Logarithms to bases other than e can be differentiated but this is outside the scope of this course.
Sometimes, the properties of logarithms, studied in year 12, are useful to help differentiate logarithmic functions.
Examples
|
a. Differentiate the function y = ln (5x) |
b. Differentiate f(x) = ln (3x2) | ||
 |
 |
||
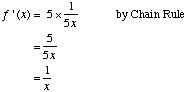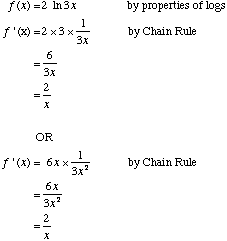c. Differentiate f(x) =  |
|
||
 |
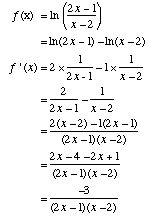