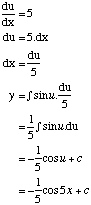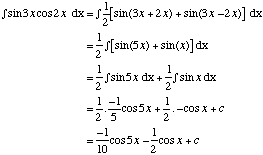The integration of trigonometric functions can be done by inspection.
The table below shows the formulae for the differentiation and integration of the basic trig. functions given to you for the Bursary examination.
|
y = f(x)
|
Integrate |
f '(x) or y ' or
 |
|
sin x
|
cos x
|
|
|
cos x
|
- sin x
|
|
|
tan x
|
sec 2x
|
|
|
sec x
|
sec x tan x
|
|
|
cosec x
|
- cosec x cot x
|
|
|
cot x
|
-cosec 2x
|
This means that if f(x) = sin x then f '(x) = cos x and therefore ∫cos x = sin x.
Integrating trigonometric functions by inspection
This is in effect a trial and error method, similar to that used with exponential functions, but becomes quite easy with practice.
To find ∫ sin 5x dx the answer could be guessed at cos 5x. However on differentiating cos 5x using the Chain
Rule we get -5sin 5x which is -5 times too big so to compensate, a factor of -1 / 5 is required.
∫ sin 5x dx =
Further example
∫ 3sin 4x dx =
Integrating trigonometric functions by substitution
Some people prefer a longer but more methodical method and the following substitution can be used.
Find ∫ sin 5x dx
Let y = ∫ sin 5x dx
and let u = 5x so y = ∫sin u dx
Integration of Trigonometric Products
Sometimes trigonometric identities are useful in integration, such as the product formulae, covered in the Trigonometry section in Topic 43, Angle Formulae.
These formulae are:
|
2sin A cos B = sin(A + B) + sin(A − B) |
|
2cos A sin B = sin(A + B) − sin(A − B)
|
|
2cos A cos B = cos(A + B) + cos(A − B)
|
|
2sin A sin B = cos(A − B) − cos(A + B)
|
Example
Find ∫ sin 3x cos 2x dx
