Expanding Brackets

cubics.jpgRemoving brackets from an expression is known as expanding the expression.

This usually occurs when a term outside a bracket is multiplied by each of the terms inside the bracket.

The outside term "distributes" itself over the inside terms. Thus the name the distributive property.

 

Distributive Property

When an expression is expanded, each term inside the bracket is multiplied by the term outside the bracket.

Example 1

3(x + 4) means       3 multiplied by (x + 4)          i.e. 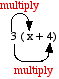Y8_Expanding_Brackets_01.gif

= 3 . x + 3 . 4 = 3p + 12

 

When brackets have been expanded, the expression must be simplified further if possible.

Example 2

5(y + 7) + 4(y + 2) 
= 5y + 35 + 4y + 8 
= 9y + 43

 

 

Further examples
Answers

Expand and simplify:

  

(a) 2(x + 7)

2(x + 7) = 2x + 14

(b) 5(3x − 6)

5(3x − 6) = 15x − 30

(c) −2(4 − 3x)

−2(4 − 3x) = −8 + 6x

(d) 4a(a − 3)

4a(a − 3) = 4a 2 − 12a

(e) 3(x + 7) + 4(x − 2)

3(x + 7) + 4(x − 2)

= 3x + 21 + 4x − 8

= 7x + 13

(f) 4x − 3(2x + 3 + 4y)

4x − 3(2x + 3 + 4y)

= 4x − 6x − 9 − 12y

= −2x − 12y − 9

Note When expanding a bracket with a NEGATIVE number in front, the signs of every term inside the bracket change.