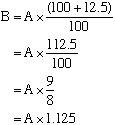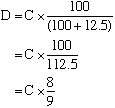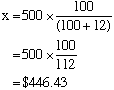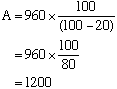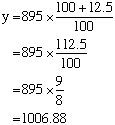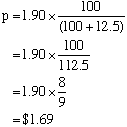A percentage is a way of writing a fraction with a denominator of 100.
x percent, written x%, means x⁄100 (or x parts out of 100)
Percentage Calculations
Below are some of the types of problem that use percentages.
Percentage of a quantity:
To find x percent of a quantity. Calculate: x⁄100 × (the quantity)
One quantity as a percentage of another quantity:
To find a out of b as a percentage. Calculate: a⁄b × 100⁄1
Increasing a quantity by a percentage:
To increase a quantity by x percent. Calculate: ![]()
Decreasing a quantity by a percentage:
To decrease a quantity by x percent. Calculate: ![]()
Percentage profit and loss:
To find the percentage profit or loss of a transaction:
Calculate for profit: ![]()
Calculate for loss: ![]()
A discount is the amount by which the price of an article is reduced.
Discount is often expressed as a percentage.
To find the cost of goods reduced by x%:
Calculate: Amount of discount = Original cost × x⁄100
New discounted cost = original cost − amount of discount
Other types of problems involving percentages include problems with interest, depreciation, inflation and commission.
|
(a) Find 8% of 300 |
(a) 300 × 8⁄100 = 24 |
|
(b) Write 13 out of 20 as a percentage. |
(b) 13⁄20 × 100⁄1 = 65% |
|
(c) Increase 50 by 8% |
(c) |
|
(d) Decrease 50 by 8% |
(d) |
|
(e) Calculate the % profit if a person buys a car for $5,000 and sells it for $6,000. |
(e) Profit is $6,000 − $5,000 = $1,000 |
|
(f) A coat is discounted at 15% . Its original cost is $90. What is its new cost? |
(f) Discount = 90 × 15⁄100 = $13.50 = $76.50 |
Finding Original Amounts
If a quantity P is increased by x% to give quantity Q then to find the original amount P:
If a quantity R is decreased by x% to give quantity S then to find the original amount R:
GST Calculations
(Goods and Services Tax, GST, is a tax used in some countries-added to the price of goods or services bought.
In some countries it is called Value-Added Tax, VAT.)
If an amount $A excludes GST at 12.5% then to find the same amount $B including GST:
If an amount $C includes GST at 12.5% to find the same amount $D excluding GST:
Examples Answers (a) An amount of money is increased by12% to give $500.
How much was the amount originally?
(a) Let the original amount be x.
The original amount was $446.43
(b) An order for a truckload of sand was decreased by 20% to 960 kg.
How much sand was originally ordered?
(b) Let the original amount of sand be A kg
The original amount of sand ordered was 1200 kg
(c) A DVD player costs $895 excluding GST at 12.5%. What would it cost including GST?
(c) Let the cost with GST be $y
The DVD player would cost $1006.88 including GST
(d) A pie costs $1,90 including GST.
What would it cost without GST?
(d) Let the cost without GST be$p
The pie would cost $1.69 without GST.