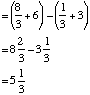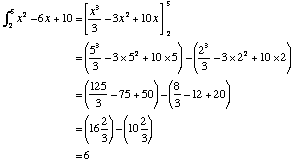The previous topic stated that integration is the opposite of differentiation. Hence its other name of anti-differentiation.
While this is true, one of the main uses of integration is to find the area between a curve and the x-axis.
These areas are found by evaluating a definite integral.
Defiinite Integrals
A definite integral is calculated by integrating a function between two values. These two values are substituted into the integrated function and the difference taken.
The formula is:
|
where F(x) is the anti-derivative of f(x) |
f(x) dx = F(b) − F(a)This complicated looking formula is easier to use than it looks. It simply means doing the following:
| Method |
Example Evaluate |
|
| Step 1 | Integrate the function | = |
| Step 2 | Substitute the values 2 and 1 |
= |
| Step 3 | Evaluate |
|
| Note that the constant of integration c is not shown as it would be eliminated when subtracting. | ||
(x2 + 3) dx
- 
Area under a Curve
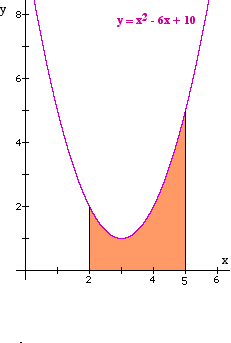
An accurate way to find the area between a curve, two x-values and the x-axis, as shaded in the example on the diagram below, is to find the definite integral between those x-values.
|
To find the shaded area between the curve f(x) = x2-6x + 10 , the lines x = 2 and x = 5 and the x-axis, evaluate the definite integral:
The shaded area is 6 square units.
|
 |
(x2 − 6x + 10) dx
It is advisable although not essential to draw a diagram before carrying out the integration.
Sometimes, when the curve crosses the x-axis, part of the area may be above the x-axis and part below the x-axis.
When this happens evaluate each area separately, treating both as positive, and then add them together.
