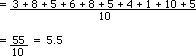When a sample has been taken, the data has to be analysed.
An average is a number that represents the centre of a set of data, or is typical of the sample.
Three types of average are commonly used: The mean, the median and the mode.
The Working with Data activity provides practice at finding measures of central tendency
The Mean of a Sample
The mean is commonly known by most people as the average.
The symbol used for the mean of a sample is 
.
The mean is calculated by adding together all of the scores or values and dividing by the number of scores or values.
If the data is in a frequency table, each score is multiplied by its frequency.
Finding the mean of a frequency distribution, including grouped data, is covered in the Frequency topic.
Findng the mean on a calculator
The procedure for finding statistical values will vary slightly from calculator to calculator.
For a typical scientific calculator, to find the mean of 5, 7, and 12:
|
Task
|
Press
|
Action
|
| Select the statistical mode |
MODE
 |
Gives three choices: COMP(1), SD(2) or REG(3) Selects SD (statistics) mode. |
| Clear old data |
   |
Always do this before entering new data. |
| Enter the data |
 DT  DT  DT |
Enters the three numbers 5, 7 and 12. |
| Find mean |
8 |
Finds the mean,  = 8 |
| Clear old data ready for next calculation |
|
Always do this after finishing a calculation. |
Pressing RCL and C on this calculator to find n is a good check to see that all values have been added.
In this case it should give n = 3.
Finding the mean on a spreadsheet
Enter the data:
The function entered in cell B5 to find the mean is =AVERAGE(A2..A5) this gives a mean of 8.
The Median
The median is the middle score or value when the data is arranged in order.
If there are an even number of scores, the median is halfway between the middle two values.
Finding the median from a set of data is covered further in Topic 46, Comparing Data.
The Mode
The mode is the most common score or value.
If all of the scores are different, there is no mode.
If the data is grouped together in a frequency table, the group with highest frequency is called themodal group or class, see Topic 47, Frequency.
|
For the following set of test results of 10 people: 3, 8, 5, 6, 8, 5, 4, 1, 10, 5 Find: (a) The mean (b) The mode (c) The median
|
(a) The mean (b) The mode = 5 (occurs 3 times) (c) Arrange in order: 1, 3, 4, 5, 5, 5, 6, 8, 8, 10 Median is 5 |
Finding Averages in a Frequency Distribution
The table shows the number of goals scored in 20 soccer games.
|
Number of goals scored in a game
|
Frequency(f)
|
|
0
|
5
|
|
1
|
7
|
|
2
|
4
|
|
3
|
3
|
|
4
|
1
|
Mode The mode is the most common score which is 1.
Median The median is the middle score which is between the 10th and 11th which is 1.
Mean To find the mean from a frequency table of ungrouped data each value is multiplied by its frequency.
|
Number of goals scored in a game
|
Frequency(f)
|
f .x
|
|
0
|
5
|
0 × 5 = 0
|
|
1
|
7
|
1 × 7 = 7
|
|
2
|
4
|
2 × 4 = 8
|
|
3
|
3
|
3 × 3 = 9
|
|
4
|
1
|
4 × 1 = 4
|
|
Totals
|
20
|
28
|
The mean, which does not have to be a whole number is 28 ÷ 20 = 1.4
If the data was grouped, the mid-points of each group would be used to find the mean.
Which average to use?
|
Average
|
Advantage
|
Disadvantage
|
|
mean
|
Uses all of the values. Can be found easily on a calculator. |
Influenced by extreme high or low values.
The value of 100 has a big effect on the mean. |
|
median
|
Not influenced by extreme high or low values.
The value of 100 does not effect the median. |
Hard to work out if there are a large number of values. |
|
mode
|
Good for finding the most popular value.
|
May not be all that representative of a set of values.
The mode is 3 which is not near the middle. |
