Roots from Graphs
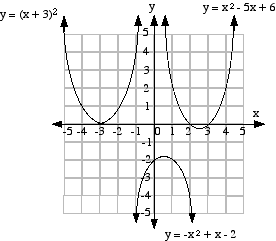
The graphs of three quadratic functions are shown below.
The roots of the corresponding quadratic equations are given by where the graph crosses the x-axis. i.e. the x- intercepts.
The roots of a quadratic equation are called real roots if the graph crosses or touches the x-axis. These roots are real numbers.
If the graph does NOT cross the x-axis the equation has no real roots. This type of equation can be solved using complex or imaginary numbers, which are usually studied in Year 12 (NZ Year 13).
| Graphs |
 |
||
| Function |
y = (x + 3)2
|
y = x2 − 5x + 6
= (x − 3)(x − 2) |
y = -x2 + x − 2
= -(x − 0.5)2 − 1.75 |
| Number and nature of the roots |
One real root
|
Two real roots
|
No real roots
|
There is a quicker way than sketching graphs or solving to determine the number of roots of a quadratic equation, this method uses the discriminant.
The Discriminant
The discriminant of a quadratic equation ax2 + bx + c = 0 is given by b2- 4ac.
The symbol, Δ is sometimes used for the discriminant.
Note that the discriminant is the part of the quadratic formula that is under the square root sign.
By examining the value of the discriminant we can determine the number and nature of the roots.
| If the discriminant is zero | b2 − 4ac = 0 | there is one (repeated) rational root |
| If the discriminant is positive | b2 − 4ac > 0 | there are two real roots |
| If the discriminant is negative | b2 − 4ac < 0 | there are no real roots |
If the discriminant is a perfect square, such as 49 or 100, then the roots will be rational (fractional) numbers.
Examples:
|
example 1
|
example 2
|
example 3
|
|
| Equation |
y = (x + 3)2 |
y = x2 − 5x + 6 | y = -x2 + x − 2 |
| a, b and c | a = 1, b = 6, c = 9 | a = 1, b = -5, c = 6 | a = -1, b = 1, c = -2 |
| Discriminant |
b2- 4ac = 62 − 4x1x9 Discriminant = 0 |
b2- 4ac = (-5)2 − 4x1x6 Discriminant = 1 |
b − 4ac = (1)2 − 4x-1x-2 Discriminant = -7 |
| Number and nature of the roots | There is one repeated real root | There are two real roots | There are no real roots |